Polinomul de interpolare Lagrange

Polinomul de interpolare Lagrange pentru 4 puncte: ((−9, 5), (−4, 2), (−1, −2), (7, 9)), L(x), care este suma polinoamelor de bază scalate y₀l₀(x), y₁l₁(x), y₂l₂(x) and y₃l₃(x). Polinomul de interpolare trece prin toate cele 4 puncte, iar fiecare polinom scalat de bază trece prin punctul său de control respectiv, în cazul în care este 0, unde x corespunde celorlalte 3 puncte. Codul Matlab pentru acest exemplu este disponibil în .

Definiție

Fie un set de k + 1 puncte de date, diferite între ele:

$(x_{0},y_{0}),\ldots ,(x_{j},y_{j}),\ldots ,(x_{k},y_{k})$

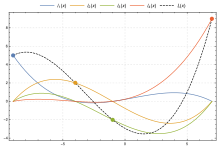
Polinomul de interpolare Lagrange este combinația liniară

$L(x):=\sum _{j=0}^{k}y_{j}\ell _{j}(x)$

de polinoame Lagrange de bază

$\ell _{j}(x):=\prod _{\begin{smallmatrix}0\leq m\leq k\\m\neq j\end{smallmatrix}}{\frac {x-x_{m}}{x_{j}-x_{m}}}={\frac {(x-x_{0})}{(x_{j}-x_{0})}}\cdots {\frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{\frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}\cdots {\frac {(x-x_{k})}{(x_{j}-x_{k})}}.$

Deși numit după Joseph Louis Lagrange în 1795, a fost descoperit pentru prima data în 1779 de către Edward Waring și a fost publicat în 1783 de Leonhard Euler.

Având în vedere ipoteza inițială că $x_{i}$ sunt diferite între ele, această expresie este întotdeauna bine definită.

Se verifică imediat că polinomul interpolează corect funcția, adică: $P(x_{i})$=$y_{i}\qquad i=0,\ldots ,k$, pentru orice i=1..n.

Exemple

1

Polinomul de interpolare al funcției tangentă

Să găsim o formulă de interpolare pentru funcția f(x) = tan(x) dată de următoarele seturi de valori:

${\begin{aligned}x_{0}&=-1.5&&&&&f(x_{0})&=-14.1014\\x_{1}&=-0.75&&&&&f(x_{1})&=-0.931596\\x_{2}&=0&&&&&f(x_{2})&=0\\x_{3}&=0.75&&&&&f(x_{3})&=0.931596\\x_{4}&=1.5&&&&&f(x_{4})&=14.1014.\end{aligned}}$

Polinoamele de bază sunt:

$\ell _{0}(x)={x-x_{1} \over x_{0}-x_{1}}\cdot {x-x_{2} \over x_{0}-x_{2}}\cdot {x-x_{3} \over x_{0}-x_{3}}\cdot {x-x_{4} \over x_{0}-x_{4}}={1 \over 243}x(2x-3)(4x-3)(4x+3)$

$\ell _{1}(x)={x-x_{0} \over x_{1}-x_{0}}\cdot {x-x_{2} \over x_{1}-x_{2}}\cdot {x-x_{3} \over x_{1}-x_{3}}\cdot {x-x_{4} \over x_{1}-x_{4}}={}-{8 \over 243}x(2x-3)(2x+3)(4x-3)$

$\ell _{2}(x)={x-x_{0} \over x_{2}-x_{0}}\cdot {x-x_{1} \over x_{2}-x_{1}}\cdot {x-x_{3} \over x_{2}-x_{3}}\cdot {x-x_{4} \over x_{2}-x_{4}}={3 \over 243}(2x+3)(4x+3)(4x-3)(2x-3)$

$\ell _{3}(x)={x-x_{0} \over x_{3}-x_{0}}\cdot {x-x_{1} \over x_{3}-x_{1}}\cdot {x-x_{2} \over x_{3}-x_{2}}\cdot {x-x_{4} \over x_{3}-x_{4}}=-{8 \over 243}x(2x-3)(2x+3)(4x+3)$

$\ell _{4}(x)={x-x_{0} \over x_{4}-x_{0}}\cdot {x-x_{1} \over x_{4}-x_{1}}\cdot {x-x_{2} \over x_{4}-x_{2}}\cdot {x-x_{3} \over x_{4}-x_{3}}={1 \over 243}x(2x+3)(4x-3)(4x+3).$

Deci polinomul de interpolare este:

${\begin{aligned}L(x)&={1 \over 243}{\Big (}f(x_{0})x(2x-3)(4x-3)(4x+3)\\&{}\qquad {}-8f(x_{1})x(2x-3)(2x+3)(4x-3)\\&{}\qquad {}+3f(x_{2})(2x+3)(4x+3)(4x-3)(2x-3)\\&{}\qquad {}-8f(x_{3})x(2x-3)(2x+3)(4x+3)\\&{}\qquad {}+f(x_{4})x(2x+3)(4x-3)(4x+3){\Big )}\\&=4.834848x^{3}-1.477474x.\end{aligned}}$

2

Să interpolăm funcția f(x) = x² pe domeniul 1 ? x ? 3, prin următoarele 3 puncte:

${\begin{aligned}x_{0}&=1&&&f(x_{0})&=1\\x_{1}&=2&&&f(x_{1})&=4\\x_{2}&=3&&&f(x_{2})&=9.\end{aligned}}$

Polinomul este:

${\begin{aligned}L(x)&={1}\cdot {x-2 \over 1-2}\cdot {x-3 \over 1-3}+{4}\cdot {x-1 \over 2-1}\cdot {x-3 \over 2-3}+{9}\cdot {x-1 \over 3-1}\cdot {x-2 \over 3-2}\\[10pt]&=x^{2}.\end{aligned}}$

3

Să interpolăm funcția f(x) = x³ pe domeniul 1 < x < 3, prin punctele:

$x_{0}=1\,$	$f(x_{0})=1\,$
$x_{1}=2\,$	$f(x_{1})=8\,$
$x_{2}=3\,$	$f(x_{2})=27\,$

Polinomul este:

${\begin{aligned}L(x)&={1}\cdot {x-2 \over 1-2}\cdot {x-3 \over 1-3}+{8}\cdot {x-1 \over 2-1}\cdot {x-3 \over 2-3}+{27}\cdot {x-1 \over 3-1}\cdot {x-2 \over 3-2}\\[8pt]&=6x^{2}-11x+6.\end{aligned}}$

Interpolarea baricentrică

Exemplu de divergență al polinomului de interpolare Lagrange

Forma Lagrange de interpolare polinomului arată caracterul liniar al polinomului de interpolare și unicitatea acestui polinom. De aceea, este de preferat în probe și argumente teoretice. Dar, după cum se poate observa din construcții, de fiecare dată când un nod x_k se modifică, toate polinoame Lagrange de bază trebuie să fie recalculate. O formă mai bună a polinomului de interpolare în practică este forma baricentrică de interpolare Lagrange formula Newton a polinomului.

Utilizând

$\ell (x)=(x-x_{0})(x-x_{1})\cdots (x-x_{k})$

putem rescrie polinoamele de bază Lagrange ca

$\ell _{j}(x)={\frac {\ell (x)}{x-x_{j}}}{\frac {1}{\prod _{i=0,i\neq j}^{k}(x_{j}-x_{i})}}$

sau, prin definirea ponderilor baricentrice

$w_{j}={\frac {1}{\prod _{i=0,i\neq j}^{k}(x_{j}-x_{i})}}$

putem scrie pur și simplu

$\ell _{j}(x)=\ell (x){\frac {w_{j}}{x-x_{j}}}$

care este denumit în mod obișnuit ca prima formă a formulei de interpolare baricentrică.

Avantajul este că această reprezentare polinomul de interpolare poate fi acum evaluat ca

$L(x)=\ell (x)\sum _{j=0}^{k}{\frac {w_{j}}{x-x_{j}}}y_{j}$

care, în cazul în care ponderile $w_{j}$ au fost pre-calculate, are nevoie doar de $\ mathcalO(n)$ (operații de evaluare $\ell (x)$ și ponderile $w_{j}/(x-x_{j})$), spre deosebire de ${\mathcal {O}}(n^{2})$ pentru evaluarea polinoamelor Lagrange de bază $\ ell_{j}(x)$ individual.

Formula de interpolare baricentrică poate fi, de asemenea, ușor de actualizat pentru a include un nod nou $x_{k+1}$ prin împărțirea nodurilor $w_{j}$, $j=0\dots k$ la$(x_{j}-x_{k+1})$ și construirea noului $w_{k+1}$ ca mai sus.

Putem simplifica și mai mult prima formă prin luarea în considerare prima interpolare baricentrică a funcției constante $g(x)\equiv 1$:

$g(x)=\ell (x)\sum _{j=0}^{k}{\frac {w_{j}}{x-x_{j}}}.$

Împărțirea $L(x)$ la $g(x)$ nu modifică interpolarea, dar conduce la rezultatul

$L(x)={\frac {\sum _{j=0}^{k}{\frac {w_{j}}{x-x_{j}}}y_{j}}{\sum _{j=0}^{k}{\frac {w_{j}}{x-x_{j}}}}}$

care este menționat ca forma a doua sau adevarata forma a formulei de interpolare baricentrică. Această formă are avantajul că $\ell (x)$ nu trebuie să fie evaluate pentru fiecare evaluare a $L(x)$.

Referințe

Bibliografie

• Constantin Ilioi, Probleme de optimizare și algoritmi de aproximare a soluțiilor, Editura Academiei Republicii Socialiste România, București, 1980.

Legături externe

• www.utgjiu.ro/math/mbuneci/book/mn2009.pdf
• http://cs.upm.ro/~bela.finta/.files/carti/Numerika.pdf Arhivat în 7 septembrie 2012, la Wayback Machine.