Teorema lui Thales (cerc)

Teorema lui Thales pentru puncte de pe un cerc afirmă că dacă oricare trei puncte $A$, $B$ și $C$ sunt puncte situate pe un cerc (conciclice) pentru care coarda ${\overline {AC}}$ este diametru, atunci unghiul $\angle {ABC}$ format de punctul B cu punctele diametral opuse este drept.

Teorema lui Thales (cerc) : dacă AC este diametrul, atunci unghiul B este unghi drept. Unghiurile α sunt subliniate cu roz, iar β cu verde

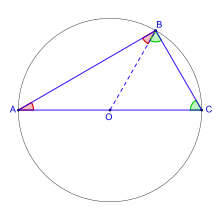
Demonstrație

Fie $O$ centrul cercului. Întrucât ${\overline {OA}}={\overline {OB}}={\overline {OC}}$, triunghiurile $\Delta {OBC}$ și $\Delta {OAB}$ sunt isoscele existând deci perechi de unghiuri congruente
$\angle {OAB}=\angle {OBA}=:\alpha$  și  $~~\angle {OBC}=\angle {OCB}=:\beta$.

Atunci unghiul B se poate scrie ca sumă
${\widehat {B}}=\alpha +\beta ={\widehat {A}}+{\widehat {C}}$

Dublul măsurii unghiurilor egale ale oricăror triunghiuri isoscele formate de raza OB e egal cu unghiurile externe de pe diametrul AC, din suma unghiurilor oricărui triunghi. Unghiurile formate de o parte a diametrului AC de raza OB sunt suplementare, suma lor constituind unghiul alungit, de măsură două unghiuri drepte.

Se obține că unghiurile A și C sunt complementare, așadar unghiul B este suma a două unghiuri complementare.

Teorema reciprocă

Locul geometric al punctelor din are A și C se văd sub același unghi drept este un cerc cu diametrul AC

„Ipotenuza unui triunghi dreptunghic este diametrul cercului său circumscris.”

Teorema împreună cu teorema reciprocă ei pot fi comasate într-un singur enunț:

„Centrul unui cerc circumscris unui triunghi se află pe una dintre laturile triunghiului dacă și numai dacă triunghiul este dreptunghic.”

Vezi și

• Teorema lui Thales