1 + 2 + 3 + 4 + …

În analiza matematică, suma tuturor numerelor naturale, 1 + 2 + 3 + 4 + ... este o serie divergentă. A n-a sumă parțială a seriei este „numărul triunghiular”

Primele patru sume parțiale ale sumei 1 + 2 + 3 + 4 + ⋯

$\sum _{k=1}^{n}k={\frac {n(n+1)}{2}},$

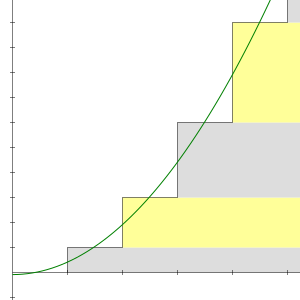
ce crește nemărginit pentru n tinzând spre infinit.

Deși, la prima vedere, poate părea că seria nu are o valoare semnificativă, suma sa poate fi manipulată pentru a produce o serie de rezultate interesante din punct de vedere matematic, dintre care unele pot folosi și în alte domenii. De exemplu, folosind funcția zeta Riemann se obține rezultatul paradoxal:

$1+2+3+4+\cdots =-{\frac {1}{12}}\,.$

În cazul particular al primelor n numere naturale, suma 1 + 2 + 3 + ... + n este ușor calculabilă:

$\sum _{k=1}^{n}k={\frac {n(n+1)}{2}}$

Suma respectivă este numită și suma lui Gauss, fiind un caz particular al sumei termenilor unei progresii aritmetice cu rația 1.

Vezi și

• 1 − 2 + 3 − 4 + · · ·
• Seria lui Grandi (1 − 1 + 1 − 1 + · · ·)

Legături externe

• This Week's Finds in Mathematical Physics (Week 124), (Week 126), (Week 147)
• Demonstrația lui Euler că 1 + 2 + 3 + · · · = −1/12