Dală

O dală este o placă poligonală subțire folosită la executarea unor pardoseli, pavaje sau placaje de zidărie.^[1] Ea este forma de bază a tuturor pavărilor matematice.

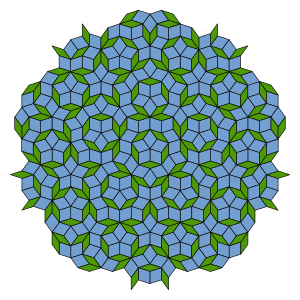
În matematică

O pavare a planului sau a oricărui alt spațiu este o acoperire a spațiului folosind un set limitat de forme, numite dale, care au interioare disjuncte. Unele dale pot fi congruente cu una sau cu mai multe altele. Dacă $S$ este mulțimea dalelor dintr-o pavare, o mulțime $R$ de forme se numește set de dale dacă nu există două forme din $R$ congruente cu oricare altele, iar fiecare dală din $S$ este congruentă cu una dintre formele din $R$ .^[2]

La o pavare este posibil să se folosească mai multe seturi diferite de dale: translația sau rotația oricăreia dintre dale produce un alt set de dale valid. Totuși, fiecare set de dale are aceeași cardinalitate, astfel încât numărul de dale este bine definit. Se spune că o pavare este monoedrică dacă are un singur tip de dală.

Aperiodicitate

O pavare care nu se repetă și folosește o singură formă, descoperită de David Smith

Se spune că un set de dale este aperiodic dacă fiecare pavare cu acele dale este o pavare aperiodică^⁠(d). În martie 2023 patru cercetători, Chaim Goodman-Strauss, David Smith, Joseph Samuel Myers și Craig S. Kaplan, au anunțat descoperirea unei dale monoedrice aperiodice și au demonstrat că dala descoperită de David Smith este aperiodică, adică o soluție la problema ein Stein^⁠(d), multă vreme nerezolvată.^[3]^[4]

Pentru dimensiuni superioare problema a fost rezolvată mai devreme: poliedrul Schmitt-Conway-Danzer este „dala” unei teselări aperiodice monoedrice a spațiului euclidian tridimensional, și care nu poate tesela spațiul în mod periodic.

Note

^ „dală” la DEX online
^ en Kaplan, Craig S. (2009), Introductory Tiling Theory for Computer Graphics, Synthesis Lectures on Computer Graphics and Animation, Morgan & Claypool Publishers, p. 7, ISBN 978-1-60845-017-6 .
^ en Roberts, Siobhan (28 martie 2023). „Elusive 'Einstein' Solves a Longstanding Math Problem”. The New York Times (în engleză). ISSN 0362-4331. Accesat în 2 iunie 2023.
^ en Smith, David; Joseph Samuel Myers; Kaplan, Craig S.; Goodman-Strauss, Chaim (2023). „An aperiodic monotile”. arXiv:2303.10798  [math.CO].

Legături externe

Portal Matematică

Materiale media legate de dală la Wikimedia Commons

[1] „dală” la DEX online

[2] Kaplan, Craig S. (2009), Introductory Tiling Theory for Computer Graphics, Synthesis Lectures on Computer Graphics and Animation, Morgan & Claypool Publishers, p. 7, ISBN 978-1-60845-017-6 .

[3] Roberts, Siobhan (28 martie 2023). „Elusive 'Einstein' Solves a Longstanding Math Problem”. The New York Times (în engleză). ISSN 0362-4331. Accesat în 2 iunie 2023.

[4] Smith, David; Joseph Samuel Myers; Kaplan, Craig S.; Goodman-Strauss, Chaim (2023). „An aperiodic monotile”. arXiv:2303.10798  [math.CO].

[1]

[2]

[3]

[4]