Metoda coardei

În analiză numerică, metoda coardei (sau metoda falsei poziții, metoda falsi) este o metodă de determinare a rădăcinii unei funcții pe un interval.

Etapele successive ale metodei falsi pe intervalul [a₁;b₁]. Rădăcina funcției este punctul marcat cu culoarea roșie

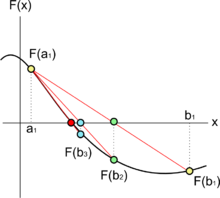
Descrierea metodei

La fel ca metoda înjumătățirii intervalului, metoda falsei poziții începe cu două puncte a₁ și b₁ astfel încât f(a₁) și f(b₁) sunt de semne opuse, ceea ce înseamnă, conform teoremei valorilor intermediare că funcția continuă f are cel puțin un zero în intervalul [a₁, b₁].

Metoda constă în producerea unui șir descrescător de intervale [a_k, b_k] care conțin rădăcina funcției f. La pasul k, este calculat numărul

$c_{k}=a_{k}-{\frac {a_{k}-b_{k}}{f(a_{k})-f(b_{k})}}f(a_{k})$

După cum se poate verifica, c_k este abscisa intersecției dreptei care trece prin punctele al liniei prin (a_k, f(a_k)) și (b_k, f(b_k)) cu axa, absciselor. Dacă f(a_k) și f(c_k) au același semn, atunci punem ak+1 = ck și bk+1 = bk; altfel, punem ak+1 = ak și bk+1 = ck.

Acest proces se repetă până când se ajunge la o valoare a funcției suficient de aproape de zero.

Pentru a verifica corectitudinea algoritmului, considerăm numerele reale a și b. Construim dreapta care trece prin punctele (a, f(a)) și (b, f(b)), ca și în contra figura alăturată. Această dreaptă este o coardă a graficului funcției f. Ecuația acestei drepte se determină folosind formula ecuației dreptei care trece printr-un punct și are o pantă dată:

$y-f(b)={\frac {f(b)-f(a)}{b-a}}(x-b).$

Se determină acum c, abscisa intersecției acestei drepte cu axa x

$f(b)+{\frac {f(b)-f(a)}{b-a}}(c-b)=0.$

Rezolvarea ecuației de mai sus oferă c_k.

Convergență

Dacă valorile inițiale a₀ și b₀ sunt luate încât f(a₀) și f(b₀) să fie de semne opuse, sunt de semn opus, atunci metoda coardei converge la un zero al lui f. Într-adevăr, din modul de construcție al intervalelor a_n și b_n, rezultă că a_n este un șir crescător, iar b_n este un șir descrescător. Ambele șiruri sunt monotone și mărginite, deci convergente. Notând cu a* - limita șirului a_n, iar cu b* - limita șirului b_n, rezultă că f(a*)<=0<=f(b*). Cel puțin unul din numerele f(a*) și f(b*) este egal cu 0, altfel pentru orice vecinătate a numărului c=(a*.f(b*)-b*.f(a*))/(f(b*)-f(a*)) ar exista un număr întreg N astfel încât pentru n>N, x_n ar aparține acestei vecinătăți, iar f(a*)<=x_n<=f(b*) pentru orice n>N, în contradicție cu convergența șirului de intervale.

Se demonstrează că dacă funcția f este strict monotonă și convexă sau concavă ($f'$ și $f''$ de semn constant), atunci viteza de convergență este superliniară, mai rapidă decât metoda înjumătățirii.

Într-adevăr, presupunem fără a restrânge generalitatea că f(a)<0 și f(b)>0 (în caz contrar, înlocuim funcția f cu -f, iar ecuația f(x)=0 ar fi echivalentă cu -f(x)=0). Deci în acest caz, funcția f este strict crescătoare, iar f'>0.

Pentru a fixa ideile, mai presupunem că f>0 la fel ca în figura de mai sus (dacă f<0 ar urma un raționament asemănător).

Deci funcția f' este strict crescătoare. Conform formulei lui Taylor, există două numere x1 și x2, astfel încât a<x1<x<x2<b, iar:

$f'(x1)={\frac {f(x)-f(a)}{x-a}}$ și $f'(x2)={\frac {f(b)-f(x)}{b-x}}$

Conform ipotezei inițiale, f'(x1)<f'(x2), de unde rezultă că

${\frac {f(b)-f(x)}{b-x}}-{\frac {f(x)-f(a)}{x-a}}<0$

După calcule elementare, această diferență este egală cu

f'(x2) - f'(x1) = ${\frac {x.(f(b)-f(a))+f(x).(a-b)-a.f(b)+b.f(a)}{(b-x).(x-a)}}$

Conform relației de calcul a lui x, se poate verifica că acesta este egal cu

$x={\frac {a.f(b)-b.f(a)}{(f(b)-f(a))}}$

Rezultă că

$f'(x2)-f'(x1)$ = ${\frac {f(x).(a-b)}{(b-x).(x-a)}}$

Deoarece a<x<b, rezultă că f(x) este de semn opus cu f'(x2) - f'(x1). În ipoteza suplimentară de convexitate, rezultă că f(x)<0.

Deci f(x) este de același semn cu f(a), iar algoritmul construiește șirul de intervale închise [a_n,b_n] astfel încât b_n=b la fiecare pas.

Pentru superliniaritate, din modul de construcție al șirului x_n, obținem

${\frac {x_{n+2}-x_{n+1}}{x_{n+1}-x_{n}}}$ = ${\frac {f(x_{n+1})}{f(x_{n})}}$ . ${\frac {f(b)-f(x_{n+1})}{f(b)-f(x_{n})}}$ . ${\frac {b-x_{n})}{b-x_{n+1}}}$

Notăm cu x* - soluția unică a ecuației. Cum x_n tinde spre x* care este diferit de b, rezultă că ultimele două fracții din membrul al doilea converg spre 1. Deci limita șirului ${\frac {x_{n+2}-x_{n+1}}{x_{n+1}-x_{n}}}$ este egală cu limita șirului ${\frac {f(x_{n+1})}{f(x_{n})}}$.

${\frac {f(x_{n+1})}{f(x_{n})}}$ = ${\frac {f(x_{n+1})-f(x*)}{x_{n+1}-x*}}$ . ${\frac {x_{n}-x*)}{f(x_{n+1})-f(x*)}}$ . ${\frac {x_{n+1}-x*}{x_{n}-x*}}$

Cum prima fracție din membrul al doilea converge spre f'(x*)>0, iar a doua fracție converge spre 1/f'(x*), rezultă că șirul ${\frac {f(x_{n+1})}{f(x_{n})}}$ are aceeași limită cu șirul ${\frac {x_{n+1}-x*}{x_{n}-x*}}$. Cum $x_{n+1}-x*$ = $x_{n}-x*$ - $f(x_{n})$ . ${\frac {b-x_{n}}{f(b)-f(x_{n})}}$, rezultă că

${\frac {x_{n+1}-x*}{x_{n}-x*}}$ = 1 - ${\frac {f(x_{n})-f(x*)}{x_{n}-x*}}$ . ${\frac {b-x_{n}}{f(b)-f(x_{n})}}$ a cărui limită este 1 - f'(x*).(b-x*)/(f(b)-f(x*)). Se observă că acest număr este cuprins între 0 și 1.

Istorie

Cele mai vechi documente care atestă cunoașterea și înțelegerea metodei falsei poziții datează cu aproximație din anul 200 î.Hr. și 200 î.Hr.. Metoda a fost găsită într-un text antic chinez numit „Nouă capitole despre arta matematicii”. Totuși, în acest text exemplele de probleme care aplică metoda falsei poziții sunt doar la ecuații liniare și soluțiile sunt atinse într-o singură etapă.

În Occident, această metodă a fost utilizat pe scară largă de către matematicienii Fibonacci, Luca Pacioli și Robert Recorde.

Pseudocod

 ''N'' ← 1
 While ''N'' ≤ ''NMAX'' 
{ 
   ''c'' ← ''a''-''f(a)''*(''b'' - ''a'')/(''f(b)'' - ''f(a)'') 
   If (''f''(''c'') = 0 or (''b'' – ''a'')/2 < ''TOL'' then 
{ 
     Output(''c'')
     Stop
}
   ''N'' ← ''N'' + 1 
   If sign(''f''(''c'')) = sign(''f''(''a'')) then ''a'' ← ''c'' else ''b'' ← ''c'' 
 }
 Output("Algoritmul nu determină soluția în numărul maxim de iterații.") 

In limbajul C++

#include<iostream.h>
#include<math.h>
#define eps 0.00000000001
#define iter 200

double f(double x)
{
return x*x*x-2*x*x*cos(x)+x-3;
}

void main()
{
unsigned char i;
double x,x0,x1,a,b,y;
cout<<"a=";cin>>a;cout<<"b=";cin>>b;
i=0;x0=a;x1=b;x=x0;y=f(x);
if (f(x0)*f(x1)<0)
	{
	while ( (i<=iter) && ((y<-eps) || (y>eps)) )
		{
		x=x0-f(x0)*(x1-x0)/(f(x1)-f(x0));
		y=f(x);
		if (f(x0)*y<0) x1=x; 
		else x0=x;
		cout<<"\n\nf("<<x<<")="<<f(x)<<" la iteratia "<<(int)i;
		i++;
		}
	if (i>iter) cout<<"problema nu se poate rezolva in nr.maxim de iteratii";
	} else cout<<"interval invalid";
}

Bibliografie

• Constantin Ilioi, Probleme de optimizare și algoritmi de aproximare a soluțiilor, Editura Academiei Republicii Socialiste România, București, 1980.

Legături externe

• www.utgjiu.ro/math/mbuneci/book/mn2009.pdf
• http://cs.upm.ro/~bela.finta/.files/carti/Numerika.pdf Arhivat în 7 septembrie 2012, la Wayback Machine.