Sector de cerc

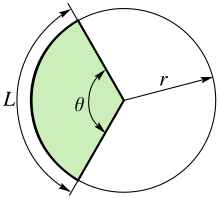
Un sector de cerc, cunoscut și ca sector circular sau, mai rar, sector de disc (simbol: ⌔), este o porțiune dintr-un disc, o zonă delimitată de un arc de cerc și două raze. Dacă unghiul dintre raze este mai mic de 180°, se vorbește despe sectorul mic, iar dacă este mai mare de 180°, se vorbește despe sectorul mare. În imaginea de alături θ este unghiul la centru, $r$ este raza cercului, iar $L$ is the lungimea arcului care mărginește sectorul mic.

Sectorul mic, colorat verde, iar cel mare rămas alb

Un sector cu unghiul la centru de 180° se numește semidisc și este delimitat de un diametru și un semicerc. Sectoarelor cu alte unghiuri la centru li se atribuie uneori nume proprii, cum ar fi cadran sau cvadrant (90°), sextant (60°) și octant (45°), fiind sectoare formate din a 4-a, a 6-a, respectiv a 8-a parte a unui disc complet. În mod confuz, arcele care le mărginesc pot fi numite la fel.

Unghiul format prin conectarea punctelor finale ale arcului la orice punct de pe circumferință care nu se află în sector este egal cu jumătate din unghiul la centru dintre razele care mărginesc sectorul.

Aria sectorului

Aria totală a unui cerc este $\pi r^{2}$. Aria sectorului poate fi obținută înmulțind aria cercului cu raportul dintre unghiul θ (exprimat în radiani) și 2π (deoarece aria sectorului este direct proporțională cu unghiul său iar 2π este unghiul întregului cerc, în radiani):

$A=\pi r^{2}\,{\frac {\theta }{2\pi }}={\frac {r^{2}\theta }{2}}$

Aria sectorului în funcție de L se poate obține înmulțind aria totală $\pi r^{2}$cu raportul dintre L și perimetrul cercului $2\pi r$:

$A=\pi r^{2}\,{\frac {L}{2\pi r}}={\frac {rL}{2}}.$

Altă abordare este prin integrare:

$A=\int _{0}^{\theta }\int _{0}^{r}dS=\int _{0}^{\theta }\int _{0}^{r}{\tilde {r}}\,d{\tilde {r}}\,d{\tilde {\theta }}=\int _{0}^{\theta }{\frac {1}{2}}r^{2}\,d{\tilde {\theta }}={\frac {r^{2}\theta }{2}}$

Exprimând unghiul la centru în grade se obține:

$A=\pi r^{2}{\frac {\theta ^{\circ }}{360^{\circ }}}$

Perimetrul sectorului

Lungimea perimetrului sectorului este suma lungimilor arcului și a celor două raze care îl mărginesc:

$P=L+2r=\theta r+2r=r(\theta +2)$

unde θ este în radiani.

Lungimea arcului

Formula lungimii arcului care mărginește sectorul este:

$L=r\theta$

unde L este lungimea arcului, r este raza cercului iar θ este unghiul la centru al arcului, în radiani. Dacă valoarea unghiului este dată în grade, relația devine:

$L=2\pi r{\frac {\theta }{360}}$

Lungimea coardei

Lungimea coardei dintre punctele extreme ale arcului este dată de:

$C=2r\sin {\frac {\theta }{2}}$

unde θ este dat în radiani.

Bibliografie

• en Gerard, L. J. V., The Elements of Geometry, in Eight Books; or, First Step in Applied Logic London: Longmans, Green, Reader and Dyer, 1874, p. 285.
• en Legendre, A. M., Elements of Geometry and Trigonometry, Charles Davies, New York: Ed. A. S. Barnes & Co., 1858), p. 119.

Vezi și

• Segment de cerc