Unghi la centru

Un unghi la centru^[1] este un unghi al cărui vârf este centrul $O$ al unui cerc și ale cărui laturi sunt raze ale cercului. În imaginea de alături razele OA și OB intersectează cercul în punctele $A$ și $B$ . Unghiul la centru subîntinde arcul dintre aceste două puncte, iar mărimea unghiului la centru, măsurat în radiani, este numeric egală cu valoarea lungimii arcului subîntins de pe cercului unitate (de rază 1).^[2] Din acest motiv unghiul la centru este cunoscut și ca distanța unghiulară a arcului subîntins de el.

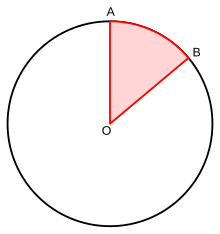
Mărimea unui unghi la centru $Θ$ este $0° < Θ < 360°$ sau $0 < Θ < 2π$ (radiani). Când se definește sau se trasează un unghi la centru, în afară de capetele sale (în imaginea de alături punctele $A$ și $B$ ) trebuie specificat dacă este vorba de arcul mic (<180°) sau de cel mare (>180°). Echivalent, se poate specifica dacă mișcarea de la punctul $A$ la punctul $B$ este în sens trigonometric sau în sens orar.

Formule

Dacă punctele $A$ și $B$ formează un diametru al cercului, atunci $Θ = 180°$ este un unghi alungit (respectiv în radiani $Θ = π$ ).

Fie $L$ arcul mic al cercului între punctele $A$ și $B$ și fie $R$ raza cercului.^[3]

Unghi la centru subîntins de arcul mic

L

Dacă unghiul la centru $Θ$ este subîntins de $L$ , atunci

0^{\circ }<\Theta <180^{\circ }\,,\,\,\Theta =\left({\frac {180L}{\pi R}}\right)^{\circ }={\frac {L}{R}}.

Demonstrație (în grade): Circumferința cercului de rază

R

este

2π R

, iar lungimea arcului mic,

L

, este proporțională din circumferință (Θ/360°). Prin urmare:

L={\frac {\Theta }{360^{\circ }}}\cdot 2\pi R\,\Rightarrow \,\Theta =\left({\frac {180L}{\pi R}}\right)^{\circ }.

Unghi la centru subîntins de arcul mare, nu de cel mic

Dacă unghiul la centru $Θ$ nu este subîntins de $L$ , atunci

180^{\circ }<\Theta <360^{\circ }\,,\,\,\Theta =\left(360-{\frac {180L}{\pi R}}\right)^{\circ }=2\pi -{\frac {L}{R}}.

Demonstrație (în radiani): Circumferința cercului de rază

R

este

2π R

, iar lungimea arcului mic,

L

, este proporțională din circumferință (Θ/2π). Prin urmare:

L={\frac {\Theta }{2\pi }}\cdot 2\pi R\,\Rightarrow \,\Theta ={\frac {L}{R}}.

Dacă tangentele în $A$ respectiv în $B$ se intersectează în punctul exterior $P$ , atunci unghiurile $∠ AOB$ și $∠ APB$ sunt suplementare (suma lor fiind 180°).

Unghiurile la centru ale poligoanelor regulate

Un poligon regulat cu $n$ laturi are un cerc circumscris pe care se află toate vârfurile sale, iar centrul cercului este, de asemenea, centrul poligonului. Unghiul la centru al poligonului regulat este format de razele la două vârfuri adiacente. Măsura acestui unghi este $2\pi /n.$

Note

^ „unghi” la DEX online
^ Clapham, C.; Nicholson, J. (2009). „Oxford Concise Dictionary of Mathematics, Central Angle” (PDF). Addison-Wesley. p. 122. Accesat în 30 decembrie 2013.
^ en „Central angle (of a circle)”. Math Open Reference. 2009. Accesat în 30 decembrie 2013. interactive

Vezi și

Unghi înscris

Legături externe

en „Central angle (of a circle)”. Math Open Reference. 2009. Accesat în 30 decembrie 2013. interactive
en „Central Angle Theorem”. Math Open Reference. 2009. Accesat în 30 decembrie 2013. interactive
en Inscribed and Central Angles in a Circle

Portal Matematică

[1] „unghi” la DEX online

[Oxford-2] Clapham, C.; Nicholson, J. (2009). „Oxford Concise Dictionary of Mathematics, Central Angle” (PDF). Addison-Wesley. p. 122. Accesat în 30 decembrie 2013.

[3] „Central angle (of a circle)”. Math Open Reference. 2009. Accesat în 30 decembrie 2013. interactive

[1]

[2]

[3]