Algoritmul Graham

Algoritmul Graham este o metodă de a găsi înfășurătoarea convexă a unui set finit de puncte din plan cu complexitatea în timp O(n log n). Este numit astfel după Ronald Graham, care a publicat algoritmul original în 1972.^[1] Algoritmul găsește toate vârfurile înfășurătoarei convexe ordonate de-a lungul frontierei sale. Folosește o stivă pentru a detecta și elimina eficient concavitățile din frontieră.

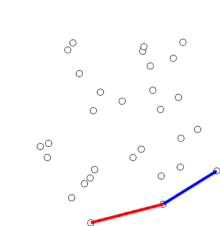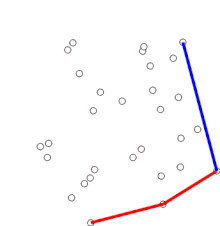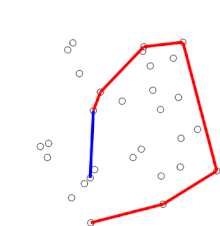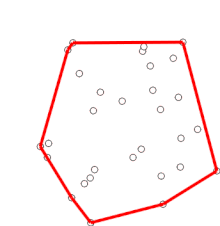
Algoritmul

După cum se poate vedea, succesiunile PAB și ABC apar în sensul invers al acelor de ceasornic, dar BCD nu. Algoritmul detectează această situație și renunță la segmentele alese anterior până când virajul este în sens invers acelor de ceasornic (ABD în acest caz)

Primul pas în acest algoritm este găsirea punctului cu cea mai mică coordonată $y$ . Dacă cea mai mică coordonată $y$ există în mai mult de un punct din set, ar trebui să fie ales punctul cu cea mai mică coordonată $x$ dintre candidați. Fie acest punct $P$ . Acest pas se face în timp O(n), unde n este numărul de puncte în cauză.

Apoi, setul de puncte trebuie sortat în ordinea crescătoare a unghiului pe care ei și punctul $P$ îl fac cu axa $x$ . Orice algoritm de sortare^⁠(d) de uz general în timp O(n log n) este potrivit pentru aceasta.

Sortarea în ordinea unghiurilor nu necesită calcularea unghiului. Este posibil să se folosească orice funcție a unghiului care este monotonă în interval $[0,\pi ]$ . Cosinusul este ușor de calculat folosind produsul scalar, sau se poate utiliza panta dreptei. Dacă este necesară precizia numerică, funcția de comparație utilizată de algoritmul de sortare poate folosi semnul produsului vectorial pentru a determina unghiurile relative.

Dacă mai multe puncte au același unghi, pentru calcule mai ușoare fie se rup legăturile prin creșterea distanței (distanța Manhattan sau distanța Cebîșev, iar distanța poate fi utilizată în locul distanței euclidiene, deoarece punctele se află pe aceeași rază), sau se elimină toate dintre acestea, cu excepția punctului cel mai îndepărtat.

Algoritmul continuă luând în ordine fiecare dintre punctele din tabloul sortat. Pentru fiecare punct se determină mai întâi dacă față de direcția deplasării dată de cele două puncte imediat anterioare direcția spre acest punct constituie un viraj la stânga sau la dreapta. Dacă virajul este la dreapta, punctul precedent nu face parte din înfășurătoarea convexă, ci se află în interiorul acesteia. Același test se face apoi pentru punct și cele două puncte care preced imediatul punctul care s-a dovedit a fi fost în interiorul înfășurătoarei, iar testul se repetă până când se întâlnește un „viraj la stânga”, moment în care algoritmul continuă cu următorul punct din setul de puncte din matricea sortată, minus punctele la care s-a găsit că sunt în interiorul înfășurătoarei. În continuare nu este nevoie ca aceste puncte să mai fie luate din nou în considerare. (Dacă în orice stadiu cele trei puncte sunt coliniare, se poate opta fie pentru a elimina pe cel intermediar, fie pentru a raporta, deoarece în unele aplicații este necesar să se găsească toate punctele de pe frontiera înfășurătoarei convexe.)

Din nou, determinarea dacă trei puncte formează un „viraj la stânga” sau un „viraj la dreapta” nu necesită calcularea unghiului real dintre cele două segmente de dreaptă și poate fi realizată prin aritmetică simplă. Pentru trei puncte $P_{1}=(x_{1},y_{1})$ , $P_{2}=(x_{2},y_{2})$ și $P_{3}=(x_{3},y_{3})$ , se calculează coordonata $z$ a produsului vectorial al celor doi vectori ${\overrightarrow {P_{1}P_{2}}}$ și ${\overrightarrow {P_{1}P_{3}}}$ , care este dat de expresia $(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1})$ . Dacă rezultatul este 0, punctele sunt coliniare; dacă este pozitiv, cele trei puncte determină o orientare de tip „viraj la stânga”, în caz contrar o orientare de tip „viraj la dreapta” (pentru punctele numerotate în sens invers al acelor de ceasornic).

Acest proces va reveni în final la punctul din care a început, moment în care algoritmul se termină și stiva conține acum punctele de pe înfășurătoarea convexă în ordinea inversă a acelor de ceasornic.

Complexitatea în timp

Sortarea punctelor are complexitatea în timp O(n log n). Deși poate părea că complexitatea de timp a buclei este O(n²), deoarece pentru fiecare punct se întoarce pentru a verifica dacă vreunul dintre punctele anterioare face un „viraj la dreapta”, ea este de fapt O(n), deoarece fiecare punct este examinat cel mult de două ori într-un anumit sens. Fiecare punct poate apărea o singură dată ca punct $(x_{2},y_{2})$ într-un „viraj la stânga” (deoarece algoritmul avansează la următorul punct $(x_{3},y_{3})$ după aceea), și ca punct $(x_{2},y_{2})$ într-un „viraj la dreapta” (caz în care punctul $(x_{2},y_{2})$ este eliminat). Complexitatea generală a timpului este prin urmare O(n log n), deoarece timpul de sortare domină timpul pentru a calcula efectiv înfășurătoare convexă.

Pseudocod

Pseudocodul de mai jos folosește o funcție ccw: ccw > 0 dacă trei puncte formează un viraj la stânga, ccw < 0 dacă formează un viraj la dreapta și ccw = 0 dacă sunt coliniare. (În aplicațiile reale, dacă coordonatele sunt numere reale arbitrare, funcția necesită comparație exactă a numerelor în virgulă mobilă și trebuie atenție la singularitățile numerice pentru punctele „aproape” coliniare.)

Rezultatul se obține în stiva stack.

let points be the list of points
let stack = empty_stack()

find the lowest y-coordinate and leftmost point, called P0
sort points by polar angle with P0, if several points have the same polar angle then only keep the farthest

for point in points:
    # pop the last point from the stack if we turn clockwise to reach this point
    while count stack > 1 and ccw(next_to_top(stack), top(stack), point) <= 0:
        pop stack
    push point to stack
end

Acum stiva conține înfășurătoarea convexă, unde punctele sunt orientate în sens invers acelor de ceasornic și P0 este primul punct.

Aici next_to_top() este o funcție care returnează intrarea din poziția imediat sub vârful stivei, fără a schimba stiva, iar top() o funcție care returnează intrarea din vârful stivei.

Acest pseudocod este adaptat după exemplul din Introduction to Algorithms.^[2]

Observații

Aceeași idee funcționează și dacă punctele sunt sortate după coordonatele $x$ în loc de unghi, iar înfășurătoarea este calculată în doi pași, pentru părțile superioară și, respectiv, inferioară. Această modificare a fost concepută de A. M. Andrew.^[3] Are aceleași caracteristici ca și algoritmul Graham.^[4]

Descrierea inițială a lui Graham a considerat sortarea pornind dintr-un punct oarecare, chiar interior înfășurătoarei convexe, nu neapărat unul dintre vârfurile acesteia.^[1] Pentru această alegere ca punct pivot pentru algoritmul de sortare, conectarea tuturor celorlalte puncte în ordinea lor sortată în jurul acestui punct produce din datele de intrare un poligon în formă de stea.^[5]

Robustețe numerică

Robustețea numerică^⁠(d) este o problemă de rezolvat în algoritmii care folosesc aritmetica în virgulă mobilă cu precizie limitată. O lucrare din 2004 a analizat o strategie incrementală simplă, care poate fi utilizată în special pentru o implementare a algoritmului Graham. Scopul lucrării nu a fost analiza algoritmului, ci furnizarea unui exemplu de manual despre cum poate eșua din cauza calculelor în virgulă mobilă.^[6] Ulterior D. Jiang și N. F. Stewart^[7] au detaliat acest aspect și folosind analiza erorilor înapoi (în engleză backward) au tras două concluzii principale. Prima este că înfășurătoarea convexă este o problemă bine condiționată^⁠(d), prin urmare este de așteptat ca algoritmii să dea un rezultat cu o marjă de eroare rezonabilă. În al doilea rând, ei au demonstrat că o modificare a algoritmului Graham pe care o numesc Graham-Fortune (încorporând ideile lui Steven Fortune pentru stabilitatea numerică^[8]) rezolvă problemele de precizie finită și de date inexacte „în măsura în care este posibil să se facă acest lucru”.

Note

^ ^a ^b en Graham, R.L. (1972). „An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set” (PDF). Information Processing Letters. 1 (4): 132–133. doi:10.1016/0020-0190(72)90045-2.
^ en Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. Introduction to Algorithms: 33.3 Finding the convex hull", (2nd ed.). MIT Press and McGraw-Hill, pp. 949–955, {{ISBN|0-262-03293-7}
^ en Andrew, A. M. (1979). „Another efficient algorithm for convex hulls in two dimensions”. Information Processing Letters. 9 (5): 216–219. doi:10.1016/0020-0190(79)90072-3.
^ en De Berg, Mark; Cheong, Otfried; Van Kreveld, Marc; Overmars, Mark (2008). Computational Geometry Algorithms and Applications . Berlin: Springer. pp. 2–14. doi:10.1007/978-3-540-77974-2. ISBN 978-3-540-77973-5.
^ en Arkin, Esther M.; Fekete, Sándor P.; Hurtado, Ferran; Mitchell, Joseph S. B.; Noy, Marc; Sacristán, Vera; Sethia, Saurabh (2003). „On the reflexivity of point sets”. În Aronov, Boris; Basu, Saugata; Pach, János; Sharir, Micha. Discrete and Computational Geometry: The Goodman-Pollack Festschrift. Algorithms and Combinatorics. 25. Berlin: Springer. pp. 139–156. doi:10.1007/978-3-642-55566-4_6. MR 2038472.
^ en Kettner, Lutz; Mehlhorn, Kurt; Pion, Sylvain; Schirra, Stefan; Yap, Chee (2008). „Classroom examples of robustness problems in geometric computations” (PDF). Computational Geometry. 40 (1): 61–78. doi:10.1016/j.comgeo.2007.06.003  . (An earlier version was reported in 2004 at ESA'2004)
^ en D. Jiang and N. F. Stewart, Backward error analysis in computational geometry Arhivat în 9 august 2017, la Wayback Machine., Computational Science and Its Applications - ICCSA 2006 Volume 3980 of the series Lecture Notes in Computer Science, pp 50-59
^ en Fortune, S. Stable maintenance of point set triangulations in two dimensions. Proceedings of the 30th annual IEEE Symposium on Foundations of Computer Science Vol. 30, 494-499, 1989.

	Portal Informatică
	Portal Matematică

[g72-1] Graham, R.L. (1972). „An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set” (PDF). Information Processing Letters. 1 (4): 132–133. doi:10.1016/0020-0190(72)90045-2.

[2] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001) [1990]. Introduction to Algorithms: 33.3 Finding the convex hull", (2nd ed.). MIT Press and McGraw-Hill, pp. 949–955, {{ISBN|0-262-03293-7}

[3] Andrew, A. M. (1979). „Another efficient algorithm for convex hulls in two dimensions”. Information Processing Letters. 9 (5): 216–219. doi:10.1016/0020-0190(79)90072-3.

[4] De Berg, Mark; Cheong, Otfried; Van Kreveld, Marc; Overmars, Mark (2008). Computational Geometry Algorithms and Applications . Berlin: Springer. pp. 2–14. doi:10.1007/978-3-540-77974-2. ISBN 978-3-540-77973-5.

[5] Arkin, Esther M.; Fekete, Sándor P.; Hurtado, Ferran; Mitchell, Joseph S. B.; Noy, Marc; Sacristán, Vera; Sethia, Saurabh (2003). „On the reflexivity of point sets”. În Aronov, Boris; Basu, Saugata; Pach, János; Sharir, Micha. Discrete and Computational Geometry: The Goodman-Pollack Festschrift. Algorithms and Combinatorics. 25. Berlin: Springer. pp. 139–156. doi:10.1007/978-3-642-55566-4_6. MR 2038472.

[mkpsy-6] Kettner, Lutz; Mehlhorn, Kurt; Pion, Sylvain; Schirra, Stefan; Yap, Chee (2008). „Classroom examples of robustness problems in geometric computations” (PDF). Computational Geometry. 40 (1): 61–78. doi:10.1016/j.comgeo.2007.06.003  . (An earlier version was reported in 2004 at ESA'2004)

[7] D. Jiang and N. F. Stewart, Backward error analysis in computational geometry Arhivat în 9 august 2017, la Wayback Machine., Computational Science and Its Applications - ICCSA 2006 Volume 3980 of the series Lecture Notes in Computer Science, pp 50-59

[8] Fortune, S. Stable maintenance of point set triangulations in two dimensions. Proceedings of the 30th annual IEEE Symposium on Foundations of Computer Science Vol. 30, 494-499, 1989.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]