Concoidă

O concoidă este o curbă derivată dintr-un punct fix O, o altă curbă și o lungime d. A fost inventată de matematicianul grec Nicomedes^⁠(d).

Concoida lui Nicomedes. Punctul fix O este punctul roșu, linia neagră este curba dată și fiecare pereche de curbe colorate este lungimea d de la intersecția cu linia pe care o face o rază în O. În cazul liniei albastre, d este mai mare decât distanța lui O față de linie, deci curba albastră superioară se arcuiește înapoi. În cazul liniei verzi, d este același, iar în cazul curbei roșii este mai mică.

Concoida lui Nicomedes desenată de un aparat, ilustrată în Comentariile lui Eutociu despre lucrările lui Arhimede

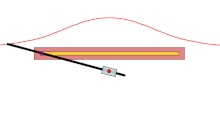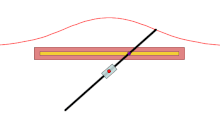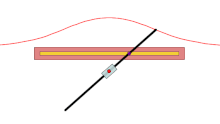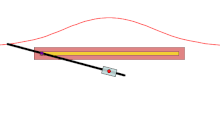
Descriere

Pentru fiecare linie prin O care intersectează curba dată în A, cele două puncte de pe linie care sunt d din A sunt pe concoidă. Concoida este, prin urmare, cisoida curbei date și un cerc de rază d și centru O. Este numită concoidă, deoarece forma ramurilor exterioare seamănă cu o concă (ghioc).

Cea mai simplă expresie folosește coordonate polare cu O la origine. Dacă

$r=\alpha (\theta )$

exprimă curba dată, atunci

$r=\alpha (\theta )\pm d$

exprimă concoida.

Dacă curba este o dreaptă, atunci concoida este concoida lui Nicomedes .

De exemplu, dacă curba este dreapta $x=a$, atunci forma polară a liniei este $r=a\sec \theta$ și, prin urmare, concoida poate fi exprimată parametric ca

$x=a\pm d\cos \theta ,\,y=a\tan \theta \pm d\sin \theta .$

Un limaçon este o concoidă cu un cerc definit ca o curbă dată.

Așa numitele concoide a lui de Sluze și a lui Dürer nu sunt de fapt concoide. Prima este o cisoidă strictă, iar cel de-al doilea este o construcție încă mai generală.

Bibliografie

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 36, 49–51, 113, 137. ISBN 0-486-60288-5. 

Vezi și

• Concoida lui de Sluze
• Cisoidă

Legături externe

Materiale media legate de concoidă la Wikimedia Commons