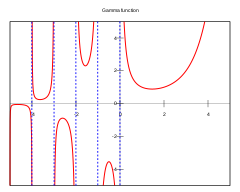
Funcția gamma
În matematică, funcția gamma, reprezentată prin litera grecească Γ = gamma majusculă, este o funcție care extinde noțiunea de factorial de la numerele întregi la numerele reale și complexe. Pentru un număr complex z cu partea reală pozitivă, funcția gamma se definește ca
Această definiție poate fi extinsă la tot restul planului complex, cu excepția numerelor întregi nepozitive.
Dacă n este un număr întreg pozitiv, atunci
ceea ce arată legătura funcției gamma cu factorialul numerelor întregi pozitive. Funcția gamma generalizează funcția factorial la valori neîntregi și complexe ale lui n.
Funcția gamma este o componentă a mai multor distribuții de probabilitate, și deci are aplicații în domeniile probabilităților, statisticii, și combinatoricii.
Definiție
modificareDefiniția principală
modificareNotația Γ(z) i se datorează lui Adrien-Marie Legendre. Dacă partea reală a numărului complex z este pozitivă (Re[z] > 0), atunci integrala
este absolut convergentă. Folosind integrarea prin părți, se poate arăta că
Această ecuație funcțională generalizează relația n! = n×(n-1)! a funcției factorial. Se poate evalua Γ(1) analitic:
Combinând aceste două relații rezultă că funcția factorial este un caz particular al funcției gamma:
pentru orice număr natural n.
Identitatea (1) poate fi folosită și pentru a extinde Γ(z) la o funcție meromorfă definită pentru toate numerele complexe z în afara lui 0 și pentru numerele întregi negative (se poate calcula că z = −n este doar un pol cu reziduul (−1)n/n!).[1] Această versiune extinsă este numită de obicei funcție gamma.
Definiții alternative
modificareUrmătoarele definiții cu produs infinit ale funcției gamma, datorate respectiv lui Euler și Weierstrass, sunt corecte pentru toate numerele complexe z, cu excepția numerelor negative:
unde γ este constanta Euler–Mascheroni.
Se poate arăta că definiția lui Euler satisface ecuația funcțională (1) de mai sus, după cum urmează. Dat fiind z diferit de 0, -1, -2, ...
Altfel, se poate arăta că:
Note
modificare- ^ George Allen, și Unwin, Ltd., The Universal Encyclopedia of Mathematics. United States of America, New American Library, Simon and Schuster, Inc., 1964. (Forward by James R. Newman)
Legături externe
modificare- Weisstein, Eric W. „Gamma Function”. MathWorld.
- Online Calculator - Funcția gamma

