Moment cinetic

Momentul cinetic (în engleză angular momentum) denumit și momentul impulsului unui corp în rotație este o mărime fizică care exprimă cantitativ (masa) și calitativ (viteza), „cantitatea transportată”. În fizica în general, este mărimea de conservare la o transformare de simetrie de rotație, conform cu teoremei lui Noether^⁠(d).

Relația dintre forță (F), momentul forței (τ) și momentul cinetic (L) în cazul unui corp în rotație

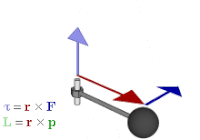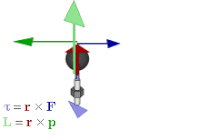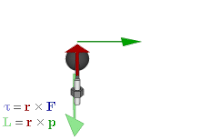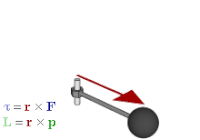
Definiție fizică

Momentul cinetic al unui punct material sau al unui corp în raport cu un punct fix într-un sistem de referință inerțial este momentul impulsului ${\vec {p}}$ al punctului material sau al corpului în raport cu acel punct la distanța ${\vec {r}}$.

Definiție matematică

Momentul cinetic este definit prin relația:

${\vec {\mathbf {L} }}={\vec {\mathbf {r} }}\times {\vec {\mathbf {p} }}$

unde:

${\vec {L}}$ - este vectorul momentului cinetic

${\vec {r}}$ - este vectorul de poziție al corpului

${\vec {p}}=m*{\vec {v}}$ - este vectorul impulsul corpului

astfel:

${\vec {L}}=m*({\vec {r}}\times {\vec {v}})$

unde:

${\vec {v}}={\vec {v}}_{r}+{\vec {\omega }}\times {\vec {v}}$ - este derivata totală (vectorială) a vectorului de poziție ${\vec {r}}$, pentru un corp rigid ${\vec {v}}_{r}=0$

Înmulțind vectorial:

${\vec {L}}/m={\vec {r}}\times ({\vec {v}}_{r}+{\vec {\omega }}\times {\vec {v}})=\omega *r^{2}*{\vec {e}}_{L}$

Mai poate fi exprimat și ca produs dintre momentul de inerție al corpului și vectorul viteză unghiulară:

${\vec {\mathbf {L} }}=I*{\vec {\boldsymbol {\omega }}}$

unde $I$ e momentul de inerție al corpului în raport cu centrul de rotație, care poate fi exprimat și ca o mărime (tensorială), și ${\vec {\omega }}$ viteza unghiulară.

Conform Teoremei Steiner, momentul de inerție se compune din momentul de inerție propriu în raport cu o axă de rotație, cât și din momentul de inerție de transport al masei.

$I=I_{0}+m*r^{2}$

Derivata temporală a momentului cinetic

Derivând momentul cinetic în raport cu timpul, se obține o mărime fizică analoagă, ca atunci când se derivează impulsul.

$d{\vec {p}}/dt={\vec {F}}=m*{\vec {a}}$ - forța, cu accelerația liniară ${\vec {a}}$

$d{\vec {L}}/dt={\vec {M}}=I*{\vec {\eta }}$ - momentul forței, cu accelerația unghiulară ${\vec {\eta }}$

Principiul conservării momentului cinetic

Într-un sistem de referință inerțial, conservarea momentului cinetic al unui corp liber în direcție și mărime este un principiu. Într-un sistem de referință neinerțial, momentul cinetic nu se conservă, ca de exemplu într-un sistem de referință în câmpul gravitațional. Acolo un corp liber câștigă impuls mărindu-și impulsul și viteza, datorită neomogenității și anizotropiei metricii neeuclidiene a spațiului în prezența câmpului gravitațional.

În virtutea teoremei Noether, de existență a unei mărimi de conservare la o transformare de simetrie, într-un spațiu omogen și izotrop euclidian, momentul cinetic este mărimea de conservare la o transformare de simetrie de rotație. Asta este valabil chiar și în mecanica cuantică. Tot așa cum energia este mărimea de conservare la o transformare de simetrie temporală, iar impulsul este mărimea de conservare la o transformare de simetrie de translație.

Într-un spațiu neomogen și anizotrop, deci cu metrică neeuclidiană, cum ar fi în câmpul gravitațional, nu există o simetrie de transformare, și ca atare acolo impulsul și astfel și momentul cinetic nu sunt conservate în niciun punct al timpului și spațiului. Ca atare, orice corp liber are o „cădere liberă” în câmpul gravitațional, mișcându-se pe o geodezică a spațiu-timpului. Cu alte cuvinte, dacă momentul cinetic nu depinde de poziția unghiulară „$\phi$” a rotației, el este conservat. Cum se poate verifica prin derivare, momentul cinetic este conservat:

cu ${\vec {\omega }}(\phi )=const$ si ${\vec {r}}(\phi )=const$ - nu depind de pozitia unghiulară $\phi$

adică:

${\vec {d}}L/d\phi =0$ - de aici rezultă - ${\vec {L}}=const$ - de unde rezultă că momentul de antrenare este - ${\vec {M}}=0$ când momentul cinetic e conservat.

Notația literală

În trecut, în literatura științifică românească și germană, momentul cinetic se nota cu litera "K". Astăzi, el se notează în literatura științifică de limbă engleză și germană cu litera "L".

Bibliografie

• S.E.Friș, A.V.Timoreva: Curs de fizică generală / Editura Tehnică 1965
• V. Vălcovici, R. Bălan, R. Voinea: Mecanica Teoretică / Editura Tehnică 1968
• E. Rebhan: Theoretische Physik / Spektrum Akademischer Verlag 1999, ISBN 3-8274-0246-8
• R.P. Feynman: Fizica Modernă, Vol.I / Editura Tehnică 1970
• R.P. Feynman, R.B Leighton, M. Sands: Lectures on Physics / Adison and Wesley 1963

Vezi și

• Momentul forței
• Teorema lui Bertrand
• Vectorul Laplace-Runge Lenz
• Rotor anticuplu
• Teorema lui Noether