În matematică inegalitatea mediilor afirmă că media aritmetică a unei liste de numere reale nenegative este mai mare sau egală cu media geometrică a aceleiași liste. În plus, că cele două medii sunt egale dacă și numai dacă toate numerele din listă sunt același (caz în care ambele medii sunt acel număr). Teorema se poate generaliza și pentru alte medii.
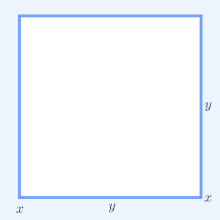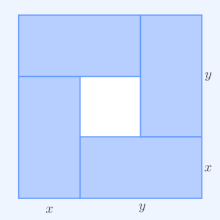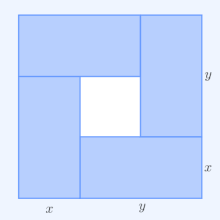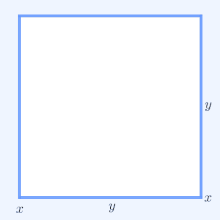
Demonstrație vizuală că (x + y )2 ≥ 4xy (media aritmetică este mai mare ca cea geometrică)[1]
Fie numerele reale strict pozitive:
a
{\displaystyle \ a}
b
{\displaystyle \ b}
x
1
{\displaystyle \ x_{1}}
x
2
{\displaystyle \ x_{2}}
x
n
{\displaystyle \ x_{n}}
Media aritmetică a numerelor
a
{\displaystyle \ a}
b
{\displaystyle \ b}
m
a
{\displaystyle \ m_{a}}
a
+
b
2
{\displaystyle {a+b} \over 2}
Generalizare : Media aritmetică a numerelor
x
1
{\displaystyle \ x_{1}}
x
2
{\displaystyle \ x_{2}}
x
n
{\displaystyle \ x_{n}}
m
a
{\displaystyle \ m_{a}}
x
1
+
x
2
+
.
.
.
+
x
n
n
{\displaystyle {x_{1}+x_{2}+...+x_{n}} \over n}
Media armonică
a
{\displaystyle \ a}
b
{\displaystyle \ b}
m
h
{\displaystyle \ m_{h}}
2
1
a
+
1
b
{\displaystyle 2 \over {{1 \over a}+{1 \over b}}}
Generalizare : Media armonică a numerelor
x
1
{\displaystyle \ x_{1}}
x
2
{\displaystyle \ x_{2}}
x
n
{\displaystyle \ x_{n}}
m
h
{\displaystyle \ m_{h}}
n
1
x
1
+
1
x
2
+
.
.
.
+
1
x
n
{\displaystyle n \over {{1 \over x_{1}}+{1 \over x_{2}}+...+{1 \over x_{n}}}}
Media geometrică a numerelor
a
{\displaystyle \ a}
b
{\displaystyle \ b}
m
g
{\displaystyle \ m_{g}}
a
⋅
b
{\displaystyle {\sqrt {a\cdot b}}}
Generalizare : Media geometrică a numerelor
x
1
{\displaystyle \ x_{1}}
x
2
{\displaystyle \ x_{2}}
x
n
{\displaystyle \ x_{n}}
m
g
{\displaystyle \ m_{g}}
x
1
⋅
x
2
⋅
.
.
.
⋅
x
n
n
{\displaystyle {\sqrt[{n}]{x_{1}\cdot x_{2}\cdot ...\cdot x_{n}}}}
Media pătratică
a
{\displaystyle \ a}
b
{\displaystyle \ b}
m
p
{\displaystyle \ m_{p}}
a
2
+
b
2
2
{\displaystyle {\sqrt {{a^{2}+b^{2}} \over 2}}}
Generalizare : Media pătratică a numerelor
x
1
{\displaystyle \ x_{1}}
x
2
{\displaystyle \ x_{2}}
x
n
{\displaystyle \ x_{n}}
m
p
{\displaystyle \ m_{p}}
x
1
2
+
x
2
2
+
.
.
.
+
x
n
2
n
{\displaystyle {\sqrt {{x_{1}^{2}+x_{2}^{2}+...+x_{n}^{2}} \over n}}}
Mediile armonică, geometrică, aritmetică și pătratică se află între a și b. Egalitatea se obține dacă a = b.
min
(
a
,
b
)
≤
m
h
≤
m
g
≤
m
a
≤
m
p
≤
max
(
a
,
b
)
{\displaystyle \min(a,b)\leq m_{h}\leq m_{g}\leq m_{a}\leq m_{p}\leq \max(a,b)}
min
(
x
1
,
x
2
,
.
.
.
,
x
n
)
≤
m
h
≤
m
g
≤
m
a
≤
m
p
≤
max
(
x
1
,
x
2
,
.
.
.
,
x
n
)
{\displaystyle \min(x_{1},x_{2},...,x_{n})\leq m_{h}\leq m_{g}\leq m_{a}\leq m_{p}\leq \max(x_{1},x_{2},...,x_{n})}
min
(
x
1
,
x
2
,
.
.
.
,
x
n
)
≤
n
1
x
1
+
1
x
2
+
.
.
.
+
1
x
n
≤
x
1
x
2
.
.
.
x
n
n
≤
x
1
+
x
2
+
.
.
.
+
x
n
n
≤
x
1
2
+
x
2
2
+
.
.
.
+
x
n
2
n
≤
max
(
x
1
,
x
2
,
.
.
.
,
x
n
)
{\displaystyle \min(x_{1},x_{2},...,x_{n})\leq {n \over {{1 \over x_{1}}+{1 \over x_{2}}+...+{1 \over x_{n}}}}\leq {\sqrt[{n}]{x_{1}\ x_{2}\ ...\ x_{n}}}\leq {{x_{1}+x_{2}+...+x_{n}} \over n}\leq {\sqrt {{x_{1}^{2}+x_{2}^{2}+...+x_{n}^{2}} \over n}}\leq \max(x_{1},x_{2},...,x_{n})}
Egalitatea 1 = x2 = ... = xn . Este atribuită lui Augustin Louis Cauchy .
Fie
a
1
,
a
2
,
⋯
,
a
n
;
λ
1
,
λ
2
,
⋯
,
λ
n
∈
R
+
.
{\displaystyle a_{1},a_{2},\cdots ,a_{n};\;\lambda _{1},\lambda _{2},\cdots ,\lambda _{n}\in \mathbb {R} _{+}.}
(
a
1
λ
1
⋅
a
2
λ
2
⋅
⋯
⋅
a
n
λ
n
)
1
λ
1
+
λ
2
+
⋯
+
λ
n
≤
λ
1
a
1
+
λ
2
a
2
+
⋯
+
λ
n
a
n
λ
1
+
λ
2
+
⋯
+
λ
n
.
{\displaystyle \left(a_{1}^{\lambda _{1}}\cdot a_{2}^{\lambda _{2}}\cdot \cdots \cdot a_{n}^{\lambda _{n}}\right)^{\frac {1}{\lambda _{1}+\lambda _{2}+\cdots +\lambda _{n}}}\leq {\frac {\lambda _{1}a_{1}+\lambda _{2}a_{2}+\cdots +\lambda _{n}a_{n}}{\lambda _{1}+\lambda _{2}+\cdots +\lambda _{n}}}.}
Demonstrație .
Fie funcția
f
:
R
+
→
R
,
f
(
x
)
=
ln
x
.
{\displaystyle f:\mathbb {R} _{+}\to \mathbb {R} ,\;f(x)=\ln x.}
f
″
(
x
)
<
0
,
(
∀
)
x
∈
R
+
,
{\displaystyle f''(x)<0,\;(\forall )x\in \mathbb {R} _{+},}
f este concavă și deci:
ln
λ
1
a
1
+
λ
2
a
2
+
⋯
+
λ
n
a
n
λ
1
+
λ
2
+
⋯
+
λ
n
≥
λ
1
ln
a
1
+
λ
2
ln
a
2
+
⋯
+
λ
n
ln
a
n
λ
1
+
λ
2
+
⋯
+
λ
n
=
{\displaystyle \ln {\frac {\lambda _{1}a_{1}+\lambda _{2}a_{2}+\cdots +\lambda _{n}a_{n}}{\lambda _{1}+\lambda _{2}+\cdots +\lambda _{n}}}\geq {\frac {\lambda _{1}\ln a_{1}+\lambda _{2}\ln a_{2}+\cdots +\lambda _{n}\ln a_{n}}{\lambda _{1}+\lambda _{2}+\cdots +\lambda _{n}}}=}
=
ln
a
1
λ
1
+
ln
a
2
λ
2
+
⋯
+
ln
a
n
λ
n
λ
1
+
λ
2
+
⋯
+
λ
n
=
ln
(
a
1
λ
1
⋅
a
2
λ
2
⋅
⋯
⋅
a
n
λ
n
)
1
λ
1
+
λ
2
+
⋯
+
λ
n
.
{\displaystyle ={\frac {\ln a_{1}^{\lambda _{1}}+\ln a_{2}^{\lambda _{2}}+\cdots +\ln a_{n}^{\lambda _{n}}}{\lambda _{1}+\lambda _{2}+\cdots +\lambda _{n}}}=\ln \left(a_{1}^{\lambda _{1}}\cdot a_{2}^{\lambda _{2}}\cdot \cdots \cdot a_{n}^{\lambda _{n}}\right)^{\frac {1}{\lambda _{1}+\lambda _{2}+\cdots +\lambda _{n}}}.}
În particular, dacă
λ
i
=
1
,
(
∀
)
i
=
1
,
n
¯
,
{\displaystyle \lambda _{i}=1,\;(\forall )i={\overline {1,n}},}
inegalitatea mediilor :
![{\displaystyle {\sqrt[{n}]{x_{1}\cdot x_{2}\cdot ...\cdot x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/355885ee566aa0a373767777c79276730c57b1c8)
![{\displaystyle \min(x_{1},x_{2},...,x_{n})\leq {n \over {{1 \over x_{1}}+{1 \over x_{2}}+...+{1 \over x_{n}}}}\leq {\sqrt[{n}]{x_{1}\ x_{2}\ ...\ x_{n}}}\leq {{x_{1}+x_{2}+...+x_{n}} \over n}\leq {\sqrt {{x_{1}^{2}+x_{2}^{2}+...+x_{n}^{2}} \over n}}\leq \max(x_{1},x_{2},...,x_{n})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88aeb25c10a56d23383f63bc3bf179c2f28d39ba)
