Teorema înălțimii
(Redirecționat de la Teorema mediei geometrice)
Teorema înălțimii într-un triunghi dreptunghic sau teorema mediei geometrice este un rezultat în geometria elementară care descrie o relație între lungimea înălțimii de pe ipotenuză într-un triunghi dreptunghic și cele două proiecții ale catetelor pe ipotenuză. Teorema spune că: Într-un triunghi dreptunghic lungimea înălțimii corespunzătoare ipotenuzei este media geometrică a lungimilor proiecțiilor catetelor pe ipotenuză.[1]
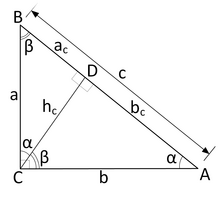

Teorema înălțimii
modificareFie CD AB , D AB , Proiecția catetei CA pe AB este AD , Iar Proiecția catetei CB pe AB este BD. (vezi figura alăturată)
sau
Formula înălțimii
modificareFie CD AB, D AB
Demonstrație (deducerea formulei): = = = =
unde: = cateta 1, = cateta 2 , = ipotenuza
Referințe
modificare- ^ Marius Perianu; Ioan Balica (). Matematică Clasa a VII-a; Semestrul al II-lea. Art educațional. p. 92. ISBN 978-606-003-340-0.
Linkuri externe
modificare- Media geometrică la tăierea nodului
