Wikipedia

Teoria statului la coadă

(Redirecționat de la Teoria statului la coadă (Queueing theory))

Teoria statului la coadă sau teoria așteptării  este studiul matematic al liniilor de așteptare, sau cozi. Modelul unei așteptări (unui stat la coadă)  este construit astfel încât lungimea cozii și timpul de așteptare pot fi prezise. Teoria așteptării este, în general, inclusă în cercetarea operațională, deoarece rezultatele sunt adesea folosite în luarea deciziilor de business în funcție de resursele necesare.

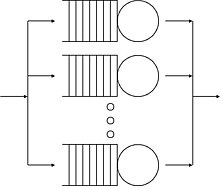
Rețelele de cozi sunt sisteme în care cozile cu un singur rând sunt conectate printr-o rețea de rutare. În această imagine, serverele sunt reprezentate prin cercuri, cozile cu o serie de dreptunghiuri, iar rețelele de rutare prin săgeți. În studierea rețelelor de cozi se încearcă, de obicei, să se obțină echilibrul distribuției în rețea, deși, în multe aplicații, fundamentală este studierea stării tranzitorii.

Teoria așteptării își are originea în cercetările lui Agner Krarup Erlang, atunci când a creat modele pentru a descrie schimbarea telefoanelor în Copenhaga. Ideile au avut multe aplicații, inclusiv în telecomunicații, ingineria traficului, de calcul[1] și, în special în ingineria industrială, în proiectarea de fabrici, magazine, birouri și spitale, precum și în managementul proiectelor.[2][3]


Nodurile unei cozi cu un singur rând

modificare

Nodurile unei cozi cu un singur rând sunt de obicei descrise cu ajutorul notației lui Kendall în formă de O/S/C, în care O descrie timpul dintre sosirile la coadă, S dimensiunea deservirilor și C numărul de servere pe nod.[4][5] În teoria așteptării, multe teoreme  pot fi demonstrate prin reducerea cozilor la sisteme matematice cunoscute sub numele de lanțuri Markov, descrise pentru prima dată de către Andrei Markov în 1906.[6]

Inginerul danez Agner Krarup Erlang și-a publicat prima sa lucrare despre ceea se numește acum  teoria așteptării, în 1909.[7][8][9] El a modelat numărul de apeluri care sosesc la un schimb într-un proces Poisson și a rezolvat coada M/D/1 în 1917 și modelul M/D/k de așteptare la coadă în 1920.[10] În notația Kendall:

  • M este pentru Markov sau fără memorie (memoryless) și înseamnă incidența sosirilor potrivit unui proces Poisson
  • D este pentru deterministic și înseamnă locurile de muncă afectate unei cozi necesitând un număr de servicii
  • k descrie numărul de servere într-un nod al unei cozi  (k = 1, 2,...). Dacă există mai multe locuri de muncă la un nodul decât există servere, atunci locurile de muncă sta la coadă și așteptând pentru servicii

Coada M/M/1 este un model simplu, în care un singur server servește locuri de muncă care sosesc potrivit unui proces Poisson și au cereri de servicii distribuite exponențial. Într-o coadă M/G/1, G înseamnă general și indică o distribuție de probabilitate arbitrară. Modelul M/G/1 a fost rezolvată de Felix Pollaczek în 1930,[11] o soluție mai târziu reformulată în termeni probabilistici de Aleksandr Khinchin și acum cunoscută sub numele de formula Pollaczek–Khinchine.

După 1940, teoria cozilor de așteptare a devenit un domeniu de cercetare de interes pentru matematicieni. În 1953, David George Kendall a rezolvat coada GI/M/k și a introdus o notație modernă pentru cozi, acum cunoscută sub numele de notația Kendall. În 1957 Pollaczek a studiat GI/G/1, folosind o  ecuație integrală. John Kingman a dat o formula pentru timpul mediu de așteptare într-o coadă G/G/1: formula Kingman.

Metoda matricei geometrice și metoda matricei analitice au permis luarea în considerare a unor cozi cu intrasosire distribuită de tip fază și cu distribuții ale timpului de deservire. Probleme precum ar fi măsurarea performanței pentru o coadă M/G/k rămâne o problemă deschisă.

Tipuri de disciplină la statul la coadă

modificare
 
Exemplu de coadă first in first out (FIFO). Enqueue = așezarea la coadă, dequeue = ieșirea din coadă.

Diferite politici de planificare pot fi folosite în nodurile de așteptare:

First in first out (Primul înăuntru primul afară)
Numit și primul-venit, primul-servit (first come, first served, FCFS),[12] acest principiu afirmă că sunt serviți clienții unul după altul și că acel client care a așteptat cel mai mult este servit primul (conform imaginii).[13]
Last in first out (Ultimul înăuntru primul afară)
Acest principiu, de asemenea, servește clienții unul după altul,, dar clientul cu cel mai scurt timp de așteptare va fi servit primul. Cunoscut și sub numele de stivă.
Partajarea procesorului
Capacitatea de deservire este împărțită în mod egal între clienți.
Prioritate
Clienții cu prioritate mare sunt serviți primii. Cozile cu priorități pot fi de două tipuri, non-preemptive (în cazul în care un loc de muncă în service nu poate fi întrerupt) și premptive (în care o deservire în curs poate fi întreruptă de o deservire cu o prioritate superioară). În niciunul dintre modele nu se pierde muncă.[14]
Shortest job first (cea mai scurtă deservire prima la rând)
Următoarea deservire este cea mai scurtă ca timp de desfășurare
Preemptive shortest job first (cea mai scurtă deservire preemptivă prima la rând)
Următoarea deservire este cea mai scurtă ca timp de desfășurare de la bun început[15]
Shortest remaining processing time (cel mai scurt timp de procesare rămas)
Următoarea deservire este cea cu cel mai scurt timp de procesare rămas.[16]
Facilitatea deservirii
  • Single server: customers line up and there is only one server
  • Parallel servers: customers line up and there are several servers
  • Tandem queue: there are many counters and customers can decide going where to queue
Comportamentul clienților la coadă
  • Balking: clienții decid să nu se mai așeze la coadă dacă este prea lungă
  • Jockeying: clienții se mută de la o coadă la alta
  • Reneging: clienții părăsesc coada de așteptare dacă au așteptat prea mult pentru a fi serviți

Rețele de cozi de așteptare

modificare
 
Exemplu de sistem de două cozi de așteptare și mai multe servere

Rețele de cozi de așteptare sunt sisteme în care un număr de cozi sunt conectate la ceea ce este cunoscut sub numele de rutarea clientului. Atunci când un client este deservit la un nod, el se poate alătura unui alt nod și unei alte cozi pentru a fi servit, sau poate părăsi rețeaua.

Pentru rețelele cu m noduri, starea sistemului poate fi descrisă printr-un vector m–dimensional (x1,x2,...,xm) unde xi reprezintă numărul de clienți la fiecare nod.

Primele rezultate semnificative în acest domeniu au fost rețelele Jackson,[17][18] pentru care există o distribuție staționară eficientă și o analiză a valorii medii[19], care permit măsurători medii, cum ar fi calculul timpilor de tranzitare și de ședere.[20] Dacă numărul total de clienți în rețea rămâne constant, rețeaua se numește rețea închisă și s-a prezentat o formă de distribuție staționară în teorema Gordon–Newell.[21] Acest rezultat a fost extins la rețeaua BCMP[22] în care o rețea cu un timp foarte general de deservire, regimurile și rutarea clienților sunt prezentate ca un produs cu formă de distribuție staționară. Constanta de normalizare poate fi calculată cu algoritmul lui Buzen, propus în 1973.[23]

Rețele de clienți au fost de asemenea investigate, rețelele Kelly, în care clienții din diferite clase experimentează diferite nivele de prioritate la diferite noduri de servicii.[24] Un alt tip de rețele sunt G-rețele, propus pentru prima dată de Erol Gelenbe în 1993:[25] Aceste rețele nu presupun exponențială timp distribuții, cum ar fi clasic Jackson Rețea.

 
Nașterea și moartea ca procese.

Algoritmi de rutare

modificare

În rețelele discrete de timp în care există o constrângere la care nodurile de deservire pot fi active la un moment dat, algoritmul programării max-greutate  alege o politica de deserviri pentru a oferi transfer optim în cazul în care fiecare loc de muncă vizitează doar un singur nod de deservire. În cel mai general caz în care locurile de muncă pot vizita mai mult de un nod, rutarea de contrapresiune oferă  transfer optim. Un programator de rețea trebuie să aleagă un algoritm de așteptare, care afectează caracteristicile unei rețele mai mari. A se vedea, de asemenea, programarea stohastică, pentru mai multe detalii despre programarea sistemelor de așteptare.

Limite medii de câmp 

modificare

Limite medii de câmp iau în considerare limitarea comportamentul limitativ al măsurătorii empirice (proporția cozilor în stări diferite), când numărul cozilor (m de mai sus) tinde spre infinit. Impactul altor cozi asupra oricărei cozi în rețea este aproximată printr-o ecuație diferențială. Modelul determinist  converge spre aceeași distribuție staționară ca și modelul original.[26]

Limite fluide

modificare

Limitele fluide sunt analogi determiniști continui ai rețelelor de așteptare obținute luarea limitei când procesul este scalat în timp și spațiu, permițând obiecte eterogene. Această traiectorie scalată  converge spre ecuație deterministă care permite demonstrarea stabilității sistemului. Este cunoscut faptul că o rețea de cozi poate fi stabilă, dar are o limită fluidă instabilă.[27]

Trafic greu / aproximări ale difuziei

modificare

Într-un sistem cu rate mari de ocupare (utilizare aproape de 1) aproximarea unui trafic intens poate fi folosită pentru a aproxima lungimea procesului de așteptare  prin reflectarea mișcării browniene (RMB),[28] procesul Ornstein–Uhlenbeck sau, mai general, procesul de difuzie.[29] Numărul de dimensiuni ale RMB este egal cu numărul nodurilor de așteptare și difuzia este limitată orthantul nenegativ.

Vezi și

modificare

Referințe

modificare
  1. ^ Lawrence W. Dowdy, Virgilio A.F. Almeida, Daniel A. Menasce. „Performance by Design: Computer Capacity Planning by Example”. 
  2. ^ Schlechter, Kira (). „Hershey Medical Center to open redesigned emergency room”. The Patriot-News. 
  3. ^ Mayhew, Les; Smith, David (decembrie 2006). Using queuing theory to analyse completion times in accident and emergency departments in the light of the Government 4-hour target. Bayes Business School (formerly Cass). ISBN 978-1-905752-06-5. Accesat în . 
  4. ^ Tijms, H.C, Algorithmic Analysis of Queues, Chapter 9 in A First Course in Stochastic Models, Wiley, Chichester, 2003
  5. ^ Kendall, D. G. (). „Stochastic Processes Occurring in the Theory of Queues and their Analysis by the Method of the Imbedded Markov Chain”. The Annals of Mathematical Statistics. 24 (3): 338. doi:10.1214/aoms/1177728975. JSTOR 2236285. 
  6. ^ A.A. Markov, Extension of the law of large numbers to dependent quantities, Izvestiia Fiz.-Matem. Obsch. Kazan Univ., (2nd Ser.), 15(1906), pp. 135–156 [Also [37], pp. 339–361].
  7. ^ „Agner Krarup Erlang (1878 - 1929) | plus.maths.org”. Pass.maths.org.uk. Accesat în . 
  8. ^ Asmussen, S. R.; Boxma, O. J. (). „Editorial introduction”. Queueing Systems. 63: 1. doi:10.1007/s11134-009-9151-8. 
  9. ^ Erlang, Agner Krarup (). „The theory of probabilities and telephone conversations” (PDF). Nyt Tidsskrift for Matematik B. 20: 33–39. Arhivat din original (PDF) la . 
  10. ^ Kingman, J. F. C. (). „The first Erlang century—and the next”. Queueing Systems. 63: 3–4. doi:10.1007/s11134-009-9147-4. 
  11. ^ Pollaczek, F., Ueber eine Aufgabe der Wahrscheinlichkeitstheorie, Math. Z. 1930
  12. ^ Manuel, Laguna (). Business Process Modeling, Simulation and Design (în engleză). Pearson Education India. p. 178. ISBN 9788131761359. Accesat în . 
  13. ^ Penttinen A., Chapter 8 – Queueing Systems, Lecture Notes: S-38.145 - Introduction to Teletraffic Theory.
  14. ^ Harchol-Balter, M. (). „Scheduling: Non-Preemptive, Size-Based Policies”. Performance Modeling and Design of Computer Systems. p. 499. doi:10.1017/CBO9781139226424.039. ISBN 9781139226424. 
  15. ^ Harchol-Balter, M. (). „Scheduling: Preemptive, Size-Based Policies”. Performance Modeling and Design of Computer Systems. p. 508. doi:10.1017/CBO9781139226424.040. ISBN 9781139226424. 
  16. ^ Harchol-Balter, M. (). „Scheduling: SRPT and Fairness”. Performance Modeling and Design of Computer Systems. p. 518. doi:10.1017/CBO9781139226424.041. ISBN 9781139226424. 
  17. ^ Jackson, J. R. (). „Networks of Waiting Lines”. Operations Research. 5 (4): 518–521. doi:10.1287/opre.5.4.518. JSTOR 167249. 
  18. ^ Jackson, James R. (). „Jobshop-like Queueing Systems”. Management Science. 10 (1): 131–142. doi:10.1287/mnsc.1040.0268. JSTOR 2627213. 
  19. ^ Reiser, M.; Lavenberg, S. S. (). „Mean-Value Analysis of Closed Multichain Queuing Networks”. Journal of the ACM. 27 (2): 313. doi:10.1145/322186.322195. 
  20. ^ Van Dijk, N. M. (). „On the arrival theorem for communication networks”. Computer Networks and ISDN Systems. 25 (10): 1135–2013. doi:10.1016/0169-7552(93)90073-D. 
  21. ^ Gordon, W. J.; Newell, G. F. (). „Closed Queuing Systems with Exponential Servers”. Operations Research. 15 (2): 254. doi:10.1287/opre.15.2.254. JSTOR 168557. 
  22. ^ Baskett, F.; Chandy, K. Mani; Muntz, R.R.; Palacios, F.G. (). „Open, closed and mixed networks of queues with different classes of customers”. Journal of the ACM. 22 (2): 248–260. doi:10.1145/321879.321887. 
  23. ^ Buzen, J. P. (). „Computational algorithms for closed queueing networks with exponential servers” (PDF). Communications of the ACM. 16 (9): 527. doi:10.1145/362342.362345. Arhivat din original (PDF) la . Accesat în . 
  24. ^ Kelly, F. P. (). „Networks of Queues with Customers of Different Types”. Journal of Applied Probability. 12 (3): 542–554. doi:10.2307/3212869. JSTOR 3212869. 
  25. ^ Gelenbe, Erol (). „G-Networks with Triggered Customer Movement”. Journal of Applied Probability. 30 (3): 742–748. doi:10.2307/3214781. JSTOR 3214781. 
  26. ^ Bobbio, A.; Gribaudo, M.; Telek, M. S. (). „Analysis of Large Scale Interacting Systems by Mean Field Method”. 2008 Fifth International Conference on Quantitative Evaluation of Systems. p. 215. doi:10.1109/QEST.2008.47. ISBN 978-0-7695-3360-5. 
  27. ^ en Bramson, M. (). „A stable queueing network with unstable fluid model”. The Annals of Applied Probability. 9 (3): 818. doi:10.1214/aoap/1029962815. JSTOR 2667284. 
  28. ^ en Chen, H.; Whitt, W. (). „Diffusion approximations for open queueing networks with service interruptions”. Queueing Systems. 13 (4): 335. doi:10.1007/BF01149260. 
  29. ^ en Yamada, K. (). „Diffusion Approximation for Open State-Dependent Queueing Networks in the Heavy Traffic Situation”. The Annals of Applied Probability. 5 (4): 958. doi:10.1214/aoap/1177004602. JSTOR 2245101. 
Adus de la https://ro.wikipedia.org/w/index.php?title=Teoria_statului_la_coadă&oldid=16338948