Vector izotrop

În matematică, fiind dat un spațiu vectorial X cu o formă pătratică asociată q un vector izotrop — numit și vector nul al formei pătratice — este un vector x ≠ 0 astfel încât q(x) = 0.

Un con nul, unde $q(x,y,z)=x^{2}+y^{2}-z^{2}$

Dacă o forma pătratică q admite un vector izotrop, atunci se numește formă pătratică izotropă. O formă pătratică care nu admite niciun vector izotrop se numește formă pătratică definită. Un spațiu pătratic (X, q) care are un vector izotrop se numește spațiu pseudoeuclidian^⁠(d).

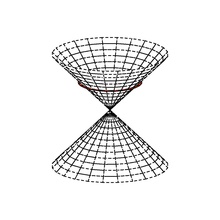
Un spațiu vectorial pseudoeuclidian poate fi descompus (neunic) în subspații ortogonale A și B astfel încât q este definită-pozitivă pe A și definită-negativă pe B. Conul izotrop (sau conul nul), al lui X constă din reuniunea sferelor echilibrate:

$\bigcup _{r\geq 0}\{x=a+b:q(a)=-q(b)=r,a\in A,b\in B\}.$

Conul izotrop este, de asemenea, reuniunea dreptelor izotrope care se intersectează în origine.

Exemple

Vectorii de tip „lumină” dintr-un spațiu Minkowski sunt vectori izotropi.

Cei patru bicuaternioni^⁠(d) independenți liniar^⁠(d) l = 1 + hi, n = 1 + hj, m = 1 + hk și m^∗ = 1 – hk sunt vectori izotropi, iar {l, n, m, m^∗} pot servi ca bază pentru subspațiul folosit pentru a reprezenta spațiu-timpul. Vectorii izotropi sunt de asemenea folosiți în abordarea formalismului Newman–Penrose^⁠(d) al varietăților spațiu-timp.

În modulul Verma^⁠(d) al unei algebre Lie^⁠(d) există vectori izotropi.

Bibliografie

• en Dubrovin, B. A.; Fomenko, A. T.; Novikov, Serghei P. (1984). Modern Geometry: Methods and Applications. Tradus de Burns, Robert G. Springer. p. 50. ISBN 0-387-90872-2. 
• en Shaw, Ronald (1982). Linear Algebra and Group Representations. 1. Academic Press. p. 151. ISBN 0-12-639201-3. 
• en Neville, Eric Harold (1922). Prolegomena to Analytical Geometry in Anisotropic Euclidean Space of Three Dimensions. Cambridge University Press. p. 204.