Reuniune (matematică)

În teoria mulțimilor, reuniunea (notată cu ∪) a unei colecții de mulțimi este mulțimea tuturor elementelor din colecție.^[1] Este una dintre operațiile fundamentale prin care mulțimile pot fi combinate și legate între ele.

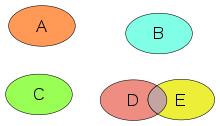
Reuniunea a două mulțimi

Reunirea a două mulțimi A și B este mulțimea de elemente care sunt în A, în B sau și în A, și în B.^[2] În simboluri:

A\cup B=\{x:x\in A{\text{  or  }}x\in B\}

.^[3]

De exemplu, dacă A = {1, 3, 5, 7} iar B = {1, 2, 4, 6, 7}, atunci A ∪ B = {1, 2, 3, 4, 5, 6, 7}. Un exemplu mai elaborat (care implică două mulțimi infinite) este:

A = {x este un întreg par mai mare ca 1}

B = {x este un întreg impar mai mare ca 1}

A\cup B=\{2,3,4,5,6,\dots \}

Ca un alt exemplu, numărul 9 nu este cuprins în reuniunea mulțimii numerelor prime {2, 3, 5, 7, 11, ...} și a mulțimii de numere pare {2, 4, 6, 8, 10 , ...}, deoarece 9 nu este nici prim și nici par.

Mulțimile nu pot avea elemente duplicate,^[3]^[4] deci reuniunea mulțimilor {1, 2, 3} și {2, 3, 4} este {1, 2, 3, 4}. Aparițiile multiple ale elementelor identice nu au niciun efect asupra cardinalității unei mulțimi sau a conținutului acesteia.

Proprietăți algebrice

Reuniunea binară este o operație asociativă; adică pentru orice mulțimi A, B și C,

A\cup (B\cup C)=(A\cup B)\cup C.

Operațiile pot fi efectuate în orice ordine, iar parantezele pot fi omise fără ambiguitate (adică oricare expresie dintre cele de mai sus poate fi exprimată echivalent ca A ∪ B ∪ C). În mod similar, reuniunea este comutativă, astfel încât mulțimile pot fi scrise în orice ordine.^[5]

Mulțimea vidă este elementul neutru pentru operația de reuniune. Adică A ∪ ∅ = A pentru orice mulțime A. Acest lucru rezultă din fapte analoage despre disjuncția logică.

Deoarece mulțimile cu uniuni și intersecții formează o algebră booleană, intersecția este distributivă pe reuniune

A\cap (B\cup C)=(A\cap B)\cup (A\cap C)

iar reuniunea este distributivă pe intersecție

A\cup (B\cap C)=(A\cup B)\cap (A\cup C)

.^[2]

În cadrul unei mulțimi universale date, reuniunea poate fi scrisă în termeni de operații de intersecție și complement ca

A\cup B=\left(A^{C}\cap B^{C}\right)^{C}

unde exponentul ^C indică complementul față de mulțimea universală. Reuniunea unei mulțimi cu ea însăși este idempotentă:

A\cup A=A

Reuniuni finite

Se poate face reuniunea mai multor mulțimi simultan. De exemplu, reuniunea a trei mulțimi A, B și C conține toate elementele lui A, toate elementele lui B, toate elementele lui C și nimic altceva. Astfel, x este un element al A ∪ B ∪ C dacă și numai dacă x este în cel puțin una dintre mulțimile A, B sau C.

O reuniune finită este reuniunea unui număr finit de mulțimi; fraza nu implică faptul ca reuniunea să fie o mulțime finită.^[6]^[7]

Reuniuni de mulțimi disjuncte

Orice mulțime se poate scrie ca reuniune a unor mulțimi disjuncte două câte două, acestea formând partiții ale mulțimii respective. Mai departe acest rezultat este încorporat în teoria probabilităților, de exemplu în teorema lui Bayes.

Reuniuni arbitrare

Noțiunea cea mai generală este reuniunea unei colecții arbitrare de mulțimi. Dacă M este o mulțime sau o clasă ale cărei elemente sunt mulțimi, atunci x este un element al reuniunii lui M dacă și numai dacă există cel puțin un element A al lui M astfel încât x să fie un element al lui A.^[8] În simboluri:

x\in \bigcup \mathbf {M} \iff \exists A\in \mathbf {M} ,\ x\in A.

Această idee rezumă secțiunile precedente — de exemplu A ∪ B ∪ C este reuniunea colecției {A, B, C}. De asemenea, dacă M este colecția vidă, atunci reuniunea lui M este o mulțime vidă.

Notații

Notația pentru conceptul general poate varia considerabil. Pentru o reuniune finită de mulțimi $S_{1},S_{2},S_{3},\dots ,S_{n}$ unii scriu adesea $S_{1}\cup S_{2}\cup S_{3}\cup \dots \cup S_{n}$ sau $\bigcup _{i=1}^{n}S_{i}$ . Diferite notații întâlnite pentru reuniunile arbitrare sunt $\bigcup \mathbf {M}$ , $\bigcup _{A\in \mathbf {M} }A$ și $\bigcup _{i\in I}A_{i}$ .^[9] Ultima dintre aceste notații se referă la reuniunea colecției $\left\{A_{i}:i\in I\right\}$ , unde I este o mulțime de indici și $A_{i}$ este câte o mulțime pentru fiecare $i\in I$ . În cazul în care mulțimea de indici I este mulțimea numerelor naturale se folosește notația $\bigcup _{i=1}^{\infty }A_{i}$ , care este analoagă cu cea a sumei infinite a unei serii.^[8]

Când simbolul "∪" este plasat în fața altor simboluri (în loc să fie între ele), de obicei simbolul este mare.

Codurile notației

În Unicode, reuniunea este reprezentată de caracterul 'UNION' (U+222A). În TeX, $\cup$ este generat din \cup.

Note

^ en Weisstein, Eric W. „Union”. Wolfram's Mathworld. Arhivat din original la 7 februarie 2009. Accesat în 14 iulie 2009.
^ ^a ^b en „Set Operations | Union | Intersection | Complement | Difference | Mutually Exclusive | Partitions | De Morgan's Law | Distributive Law | Cartesian Product”. www.probabilitycourse.com. Accesat în 5 septembrie 2020.
^ ^a ^b en Vereshchagin, Nikolai Konstantinovich; Shen, Alexander (1 ianuarie 2002). Basic Set Theory. American Mathematical Soc. ISBN 9780821827314.
^ en deHaan, Lex; Koppelaars, Toon (25 octombrie 2007). Applied Mathematics for Database Professionals. Apress. ISBN 9781430203483.
^ en Halmos, P. R. (27 noiembrie 2013). Naive Set Theory. Springer Science & Business Media. ISBN 9781475716450.
^ en Dasgupta, Abhijit (11 decembrie 2013). Set Theory: With an Introduction to Real Point Sets. Springer Science & Business Media. ISBN 9781461488545.
^ en „Finite Union of Finite Sets is Finite - ProofWiki”. proofwiki.org. Arhivat din original la 11 septembrie 2014. Accesat în 29 aprilie 2018.
^ ^a ^b en Smith, Douglas; Eggen, Maurice; Andre, Richard St (1 august 2014). A Transition to Advanced Mathematics. Cengage Learning. ISBN 9781285463261.
^ en „Comprehensive List of Set Theory Symbols”. Math Vault. 11 aprilie 2020. Accesat în 5 septembrie 2020.

Legături externe

Materiale media legate de reuniune la Wikimedia Commons
en Union of sets, Encyclopedia of Mathematics, Springer
en Infinite Union and Intersection, la ProvenMath, De Morgan's laws formally proven from the axioms of set theory.

Portal Matematică

[1] Weisstein, Eric W. „Union”. Wolfram's Mathworld. Arhivat din original la 7 februarie 2009. Accesat în 14 iulie 2009.

[:3-2] „Set Operations | Union | Intersection | Complement | Difference | Mutually Exclusive | Partitions | De Morgan's Law | Distributive Law | Cartesian Product”. www.probabilitycourse.com. Accesat în 5 septembrie 2020.

[:0-3] Vereshchagin, Nikolai Konstantinovich; Shen, Alexander (1 ianuarie 2002). Basic Set Theory. American Mathematical Soc. ISBN 9780821827314.

[4] Haan, Lex; Koppelaars, Toon (25 octombrie 2007). Applied Mathematics for Database Professionals. Apress. ISBN 9781430203483.

[5] Halmos, P. R. (27 noiembrie 2013). Naive Set Theory. Springer Science & Business Media. ISBN 9781475716450.

[6] Dasgupta, Abhijit (11 decembrie 2013). Set Theory: With an Introduction to Real Point Sets. Springer Science & Business Media. ISBN 9781461488545.

[7] „Finite Union of Finite Sets is Finite - ProofWiki”. proofwiki.org. Arhivat din original la 11 septembrie 2014. Accesat în 29 aprilie 2018.

[:1-8] Smith, Douglas; Eggen, Maurice; Andre, Richard St (1 august 2014). A Transition to Advanced Mathematics. Cengage Learning. ISBN 9781285463261.

[:2-9] „Comprehensive List of Set Theory Symbols”. Math Vault. 11 aprilie 2020. Accesat în 5 septembrie 2020.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]