Geometrie moleculară
Termenul de geometrie moleculară face referire la aranjamentul tridimensional al atomilor în cadrul unei molecule. Geometria moleculară influențează unele proprietăți ale unei substanțe, printre care cele mai importante sunt: reactivitatea, polaritatea, starea de agregare, culoarea, proprietățile magnetice și activitatea biologică.[1][2][3]
Determinare
modificareÎn prezent, cel mai folosit model teoretic care ajută la determinarea geometriei moleculare este teoria repulsiilor perechilor de electroni din stratul de valență, care susține că numărul perechilor de electroni neparticipanți din anumiți atomi influențează aranjarea tridimensională a atomilor din moleculă.
Tipuri de geometrii
modificareUnghiul de legătură este unghiul dintre două legături adiacente. Printre cele mai comune geometrii moleculare se numără:
- Liniară: Atomii dintr-o moleculă sunt aranjați pe o linie dreaptă, iar unghiurile de legătură sunt de 180°. Exemple: dioxid de carbon, oxid nitric.
- Trigonal-planară: Atomii formează o geometrie triunghiulară, iar ca și consecință molecula va fi planară și unghiurile de legătură vor fi de 120°. Exemplu: trifluorură de bor.
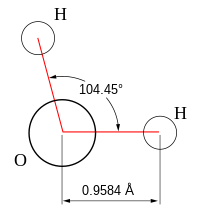
- Unghiulară: Moleculele unghiulare sunt cele a căror formă nu este liniară. Exemplu: apa (H2O), care are un unghi de legătură de 105°. Geometria aceasta este datorată celor două perechi de electroni neparticipanți de la atomul de oxigen.
- Tetraedrică: Atomii sunt aranjați în vârfurile unui tetraedru, cu un atom central care se află în interior. Unghiurile de legătură sunt de 109,47°. Exemplu: metan (CH4).
- Octaedrică: Atomii sunt aranjați în vârfurile unui octaedru, cu un atom central care se află în interior. Unghiurile de legătură sunt de 90°. Exemplu: hexafluorură de sulf (SF6).
- Trigonal-piramidală: Atomii sunt aranjați în vârfurile unei piramide trigonale (adică cu baza triunghiulară). Exemplu: amoniac (NH3), a cărei geometrie este datorată de perechea de electroni neparticipanți de la atomul de azot.[4]
Modelul RPESV
modificareUnghiurile de legătură din tabelul următor sunt unghiurile ideale prevăzute de teoria repulsiilor perechilor de electroni din stratul de valență, iar în paranteză sunt trecute unghiurile adevărate corespunzătoare pentru exemplele date.
| Nr. atomi legați de atomul central |
Perechi de electroni neparticipanți |
Domenii electronice (număr steric) |
Geometria | Unghi de legătură ideal (pentru exemplu) |
Exemplu | Imagine |
|---|---|---|---|---|---|---|
| 2 | 0 | 2 | liniară | 180° | CO2 | |
| 3 | 0 | 3 | trigonal-planară | 120° | BF3 | |
| 2 | 1 | 3 | unghiulară | 120° (119°) | SO2 | |
| 4 | 0 | 4 | tetradrică | 109.5° | CH4 | |
| 3 | 1 | 4 | trigonal-piramidală piramidă triunghiulară |
109.5 (107.8°) | NH3 | |
| 2 | 2 | 4 | unghiulară | 109.5° (104.48°)[5][6] | H2O | |
| 5 | 0 | 5 | trigonal-bipiramidală bipiramidă triunghiulară |
90°, 120°, 180° | PCl5 | |
| 4 | 1 | 5 | tetraedru deformat | ax–ax 180° (173.1°), eq–eq 120° (101.6°), ax–eq 90° |
SF4 | |
| 3 | 2 | 5 | formă-T | 90° (87.5°), 180° (175°) | ClF3 | |
| 2 | 3 | 5 | linear | 180° | XeF2 | |
| 6 | 0 | 6 | octaedrică | 90°, 180° | SF6 | |
| 5 | 1 | 6 | piramidă pătrată | 90° (84.8°) | BrF5 | |
| 4 | 2 | 6 | pătrat plan plan-pătrat |
90°, 180° | XeF4 | |
| 7 | 0 | 7 | pentagonal-bipiramidală | 90°, 72°, 180° | IF7 | |
| 6 | 1 | 7 | pentagonal-piramidală | 72°, 90°, 144° | XeOF5− | |
| 5 | 2 | 7 | planar-pentagonală | 72°, 144° | XeF5− | |
| 8 | 0 | 8 | antiprismă pătrată | XeF82− | ||
| 9 | 0 | 9 | trigonal-prismatic | ReH92− |
Vezi și
modificareReferințe
modificare- ^ McMurry, John E. (1992), Organic Chemistry (ed. 3), Belmont: Wadsworth, ISBN 0-534-16218-5
- ^ Cotton, F. Albert; Wilkinson, Geoffrey; Murillo, Carlos A.; Bochmann, Manfred (1999), Advanced Inorganic Chemistry (ed. 6), New York: Wiley-Interscience, ISBN 0-471-19957-5
- ^ Alexandros Chremos; Jack F. Douglas (). „When does a branched polymer become a particle?”. J. Chem. Phys. 143: 111104. Bibcode:2015JChPh.143k1104C. doi:10.1063/1.4931483.
- ^ Miessler G.L. and Tarr D.A. Inorganic Chemistry (2nd ed., Prentice-Hall 1999), pp.57-58
- ^ Hoy, AR; Bunker, PR (). „A precise solution of the rotation bending Schrödinger equation for a triatomic molecule with application to the water molecule”. Journal of Molecular Spectroscopy. 74: 1–8. Bibcode:1979JMoSp..74....1H. doi:10.1016/0022-2852(79)90019-5.
- ^ CCCBDB Experimental bond angles page 2, cccbdb.nist.gov, arhivat din original la , accesat în