Melcul lui Pascal

În geometrie melcul lui Pascal este o curbă ruletă formată de traiectoria unui punct aflat pe un cerc atunci când acel cerc se rostogolește în jurul exteriorului unui cerc de aceeași rază. De asemenea, poate fi definită ca ruleta formată atunci când un cerc se rostogolește în jurul unui cerc cu jumătate din raza sa, astfel încât cercul mai mic să fie în interiorul cercului mai mare. Astfel, ele aparțin familiei de curbe numite trohoide centrate; mai precis, ele sunt epitrohoide. Cardioida este cazul particular în care punctul care generează ruleta se află pe cercul care se rostogolește. Curba rezultată are un punct de întoarcere.

Construcția melcului r = 2 + cos(π – θ)
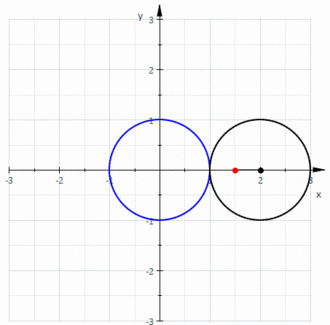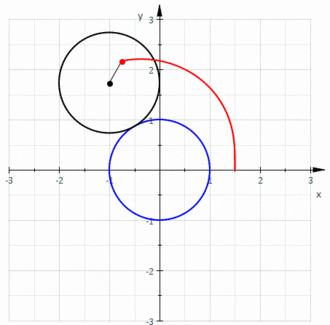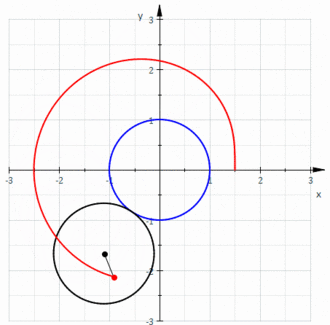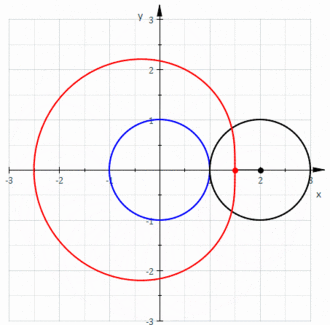
cu originea coordonatelor polare în (x, y) = (1/2, 0)

În funcție de poziția punctului care generează curba, acesta poate avea bucle interioare și exterioare (dând numele familiei), poate avea formă de inimă^⁠(d) sau poate fi oval.

Melcul lui Pascal este o curbă algebrică bicirculară plană rațională de gradul al patrulea.

Trei melci: cu adâncitură, cu punct de întoarcere (cardioidă) și cu buclă.
Melcul convex este reprezentat în imaginea de la începutul articolului.

Istoric

Cele mai vechi cercetări despre acești melci sunt în general atribuite lui Étienne Pascal, tatăl lui Blaise Pascal. Totuși, unele investigații cu privire la acestea au fost întreprinse anterior de artistul german din Renaștere Albrecht Dürer. Underweysung der Messung (în română Instrucțiuni de măsurare) a lui Dürer conține metode geometrice specifice pentru producerea de astfel de melci. Curba a fost denumită de Gilles de Roberval când a folosit-o ca exemplu pentru găsirea dreptelor tangente.

Ecuații

Ecuația (fără a fi translată sau rotită) melcului lui Pascal în coordonate polare are forma

$r=b+a\cos \theta .$

Aceasta poate fi convertită în coordonate carteziene înmulțind cu r (introducând astfel un punct în origine care în unele cazuri este fals) și înlocuind $r^{2}=x^{2}+y^{2}$ și $r\cos \theta =x$ pentru a obține

$\left(x^{2}+y^{2}-ax\right)^{2}=b^{2}\left(x^{2}+y^{2}\right).$

Aplicând forma parametrică la conversia polarelor în carteziene, se obține

$x=(b+a\cos \theta )\cos \theta ={a \over 2}+b\cos \theta +{a \over 2}\cos 2\theta ,$

$y=(b+a\cos \theta )\sin \theta =b\sin \theta +{a \over 2}\sin 2\theta ;$

punând

$z=x+iy=(b+a\cos \theta )(\cos \theta +i\sin \theta )$

se obține această parametrizare ca o curbă în planul complex:

$z={a \over 2}+be^{i\theta }+{a \over 2}e^{2i\theta }.$

Dacă ar fi deplasată orizontal cu ${\textstyle -{\frac {1}{2}}a}$, adică

$z=be^{it}+{a \over 2}e^{2it}$,

prin schimbarea originii s-ar obține forma obișnuită a ecuației unei trohoide centrate. De notat modificarea variabilei independente în acest moment pentru a clarifica faptul că nu se mai folosește parametrizarea implicită a coordonatelor polare $\theta =\arg z$.

Cazuri particulare

În cazul particular $a=b$, ecuația polară este

$r=b(1+\cos \theta )=2b\cos ^{2}{\frac {\theta }{2}}$

sau

$r^{1 \over 2}=(2b)^{1 \over 2}\cos {\frac {\theta }{2}},$

devenind un membru al familiei de spirale sinusoidale. Această curbă este cardioida.

În cazul particular $a=2b$, forma ecuației trohoidei centrate devine

$z=b\left(e^{it}+e^{2it}\right)=be^{3it \over 2}\left(e^{it \over 2}+e^{-it \over 2}\right)=2be^{3it \over 2}\cos {t \over 2},$

sau, în coordonate polare

$r=2b\cos {\theta \over 3}$

devenind un membru al familiei de rozete^⁠(d). Această curbă este o trisectoare și uneori este numită melc trisector^⁠(d).

Formă

Când $b>a$, melcul este o curbă simplă închisă. Originea satisface ecuația carteziană de mai sus, deci graficul acestei ecuații are un punct singular sau un punct izolat.

Când $b>2a$, aria mărginită de curbă este convexă, iar când $a<b<2a$, curba are o adâncitură mărginită de două puncte de inflexiune. Când $b=2a$, punctul $(-a,0)$ este un punct de curbură 0.

Pe măsură ce $b$ descrește spre $a$, adâncitura devine tot mai pronunțată până când, pentru $b=a$, curba devine o cardioidă, iar adâncitura este un punct de întoarcere. Pentru $0<b<a$, adâncitura se extinde cu o buclă interioară, iar curba se autointersectează în origine. Pe măsură ce $b$ se apropie de 0, bucla umple curba exterioară și, la limită, melcul devine un cerc parcurs de două ori.

Lectură suplimentară

• en Jane Grossman, Michael Grossman, "Dimple or no dimple", The Two-Year College Mathematics Journal, January 1982, pages 52–55.
• en Howard Anton, Calculus, 2nd edition, page 708, John Wiley & Sons, 1984.
• en Howard Anton, [1] pp. 725–726.
• en Howard Eves. A Survey of Geometry, Volume 2 (pages 51,56,273), Allyn and Bacon, 1965.

Legături externe

• Materiale media legate de melcul lui Pascal la Wikimedia Commons
• "Limacon of Pascal" at The MacTutor History of Mathematics archive
• "Limaçon" at www.2dcurves.com
• "Limaçon of Pascal" at MathCurve