Planul complex
În matematică, planul complex sau planul z este o reprezentare geometrică a numerelor complexe într-un plan geometric definit de axa reală și axa imaginară, ortogonale. El poate fi asemuit planului cartezian, cu reprezentarea părții reale a unui număr complex de-a lungul axei x, iar a părții imaginare de-a lungul axei y.



Conceptul de plan complex permite interpretarea geometrică și trigonometrică (formula lui Euler, formula lui Moivre) a numerelor complexe și folosirea lor în probleme de geometrie. În figura alăturată, distanța de-a lungul liniei albastre de la origine până la punctul z este modulul lui z, iar unghiul φ este argumentul lui z. Adunarea a două numere complexe se face la fel ca adunarea vectorilor. În coordonate polare, modulul produsului a două numere complexe produsului este produsul modulelor, iar argumentul produsului este suma argumentelor celor două numere. În particular, înmulțirea unui număr complex cu modul 1 este o rotație.
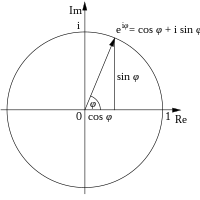
Numerele complexe de modul unu sunt situate pe un cerc trigonometric. Totalitatea sau mulțimea numerelor complexe de același modul și argumente din intervalul [0, 2π] diferite constituie un loc geometric ca cerc de rază egală cu modulul numărului.
Uneori planul complex este numit și planul Argand deoarece este folosit în diagramele Argand. Acestea sunt numite după Jean Robert Argand (1768–1822).[1] Folosită pentru vizualizarea dreptei complexe, diagrama Argand se bazează pe faptul că un număr complex poate fi reprezentat ca o pereche ordonată de numere reale. Riguros spus: corpul numerelor complexe (dreapta complexă) este un spațiu vectorial de dimensiune doi (planul real) peste sub-corpul numerelor reale.
Reprezentarea prin coordonate
modificarePlanul complex permite formularea unei geometrii analitice în coordonata complexă z similare geometriei analitice bazate pe coordonate carteziene și polare.[2][necesită sursă mai bună]
Dreapta complexă, ca orice altă dreaptă, este determinată (prin coordonate) de două puncte 0 și 1. Diferență dintre planul real și dreapta complexă apare din faptul că planul real are nevoie de trei puncte pentru a fi determinat (prin coordonate) : (0,0), (1,0) și (0,1).
Însă o dată stabilită polaritatea lui i (cu plus sau cu minus) și asocierea lui cu (0,1), planul real, în înțelesul geometric, oferă o bună reprezentare pentru numerele complexe.
Diferența dintre planul real și dreapta complexă apare mai evident atunci când se completează cele două structuri până la proiectivitate:
- pentru a deveni un plan proiectiv(d), planul real mai are nevoie în plus de o dreaptă de la infinit (a orizontului) și de un punct de la infinit.
- pentru a deveni o dreaptă proiectivă complexă (corp complet), dreapta proiectivă mai are nevoie de un singur punct, punctul de la infinit.
Planul complex în demonstrații geometrice
modificareÎn consecință, orice teoremă din geometria plană clasică poate avea și o demonstrație cu numere complexe, alături de una analitică și una vectorială.