Cardioidă

În geometrie, cardioida este o epicicloidă cu o cuspidă. Cardioida este o curbă plană descrisă de un punct de pe un cerc în timp ce acesta se rostogolește, fără alunecare, pe un alt cerc fix, exterior și de aceeași rază.

Curba roşie este o cardioidă.

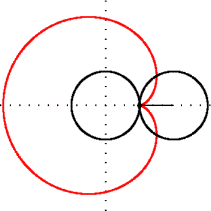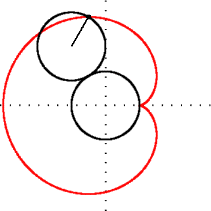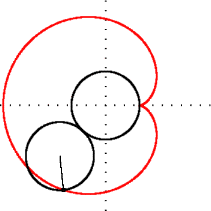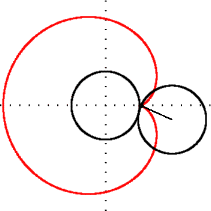
Cardioida este, de asemenea, și un caz particular al melcului lui Pascal: este un melc cu o cuspidă. Cuspida este formată atunci când raportul dintre a și b din ecuație este echiunitar.

Cardioida a fost studiată de Römer în 1674, utilizată de Vaumesle în 1678 și J. Koërsma în 1689, dar denumirea a fost propusă de G. Castilion în 1741. Numele ei provine de la forma asemănătoare unei inimi (gr. kardioeides: kardia, "inimă" și eidos, "formă"). Comparată cu simbolul care reprezintă inima (♥), se observă că inima are două vârfuri ascuțite, pe când cardioida numai unul. Este mai degrabă asemănătoare cu secțiunea transversală printr-o prună.

Cardioida este transformata inversă a parabolei.

Figura mare, centrală, din mulțimea lui Mandelbrot este o cardioidă.

Ecuații

Deoarece cardioida este o epicicloidă cu o cuspidă, are ecuațiile parametrice

$x(t)=2r\left(\cos t-{1 \over 2}\cos 2t\right),$

$y(t)=2r\left(\sin t-{1 \over 2}\sin 2t\right)$

unde r este raza cercurilor care generează curba, iar cercul fix are centrul în origine. Vârful se află la coordonatele (r,0).

Ecuația carteziană este:

$(x^{2}+y^{2}-ax)^{2}=a^{2}(x^{2}+y^{2}),$

unde a este diametrul cercului mobil.

Ecuația polară

$\rho (\theta )=2r(1-\cos \theta ).\$

descrie o cardioidă de aceeași formă. Este aceeași curbă cu cea dată mai sus, mutată la stânga cu r unități de măsură, astfel încât vârful se află în origine.

Dacă se consideră drept pol punctul de întoarcere al cardioidei, ecuația polară devine:

$\rho =a(1+\cos \theta ).$

Pentru demonstrație, vezi Demonstrații asupra cardioidei.

Grafice

Patru grafice reprezentând cardioide orientate în cele patru direcții cardinale, cu ecuațiile polare proprii.

Formule

Lungimea cardioidei este $L=8a.$

Suprafața unei cardioide cu ecuația polară

$\rho (\theta )=a(1-\cos \theta )$

este

$A={3 \over 2}\pi a^{2}$.

Vezi demonstrație.

Vezi și

• Bara lui Wittgenstein
• microfon - o discuție despre microfoane cardioide

Referințe

• Hearty Munching despre Cardioide la cut-the-knot
• Xah Lee, Cardioid (1998) (Acest sit oferă mai multe construcții alternative).
• Jan Wassenaar, Cardioid, (2005)