Poliabolo
În matematica recreativă, un poliabolo este un tiponim pentru o figură geometrică formată prin lipirea de triunghiuri dreptunghice isoscele latură la latură, formând o poliformă cu triunghiul dreptunghic isoscel ca formă de bază. Poliabolourile au fost introduse de Martin Gardner în iunie 1967, în rubrica sa de jocuri matematice din Scientific American.[1]
Etimologie
modificareForma în limba engleză, polyabolo este derivată pornind de la jucăria diabolo, deși forma rezultată prin unirea a două triunghiuri doar printr-un vârf nu este de fapt un poliabolo. Printr-o falsă analogie, interpretând di-ul inițial drept prefixul di- din limba greacă Gardner a propus denumirile figurilor formate din unul până la zece triunghiuri: monabolo, diabolo, triabolo, tetrabolo, pentabolo, hexabolo, heptabolo, octabolo, eneabolo și decabolo. Pentru a respecta construcția, accentul cade pe a.
Enumerare
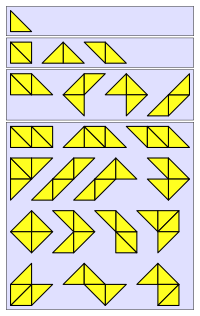
modificareExistă două moduri în care un pătrat dintr-un poliabolo poate fi format din două triunghiuri dreptunghice isoscele, dar poliabolourile sunt considerate echivalente dacă au aceleași laturi. Numărul de poliabolouri neechivalente formate din 1, 2, 3, … triunghiuri este 1, 3, 4, 14, 30, 107, 318, 1116, 3743, …[2].
Poliabolourile care se limitează strict la plan și nu pot fi răsturnate se numesc „unilaterale”. Numărul de poliabolourilor unilaterale formate din 1, 2, 3, … triunghiuri este 1, 4, 6, 22, 56, 198, 624, 2182, 7448, …[3]
La fel ca la poliomino, un poliabolo care nu poate fi nici răsturnat, nici rotit poate fi numit fix. Un poliabolo fără simetrii (de rotație sau reflexie) corespunde la 8 poliabolouri fixe distincte.
Un poliabolo care nu este simplu conex este unul care are una sau mai multe găuri în el. Cea mai mică valoare a lui n pentru care un n-abolo nu este simplu conex este 7.
Pavarea dreptunghiurilor cu dale poliabolo de un singur tip
modificareÎn 1968, David A. Klarner a definit ordinul unui poliomino. Similar, ordinul unui poliabolo P poate fi definit ca numărul minim de copii congruente ale lui P care pot fi asamblate (permițând translația, rotația și reflexia) pentru a forma un dreptunghi. Un poliabolo are ordinul 1 dacă și numai dacă este el însuși dreptunghi. Poliabolourile de ordinul 2 sunt, de asemenea, ușor de recunoscut. Solomon W. Golomb a găsit poliabolouri, inclusiv un triabolo, de ordinul 8.[4] Michael Reid a găsit un heptabolo de ordinul 6.[5] Sunt posibile ordine superioare.
Există pavări interesante cu poliabolouri ale planului euclidian. Una dintre acestea este pavarea pătrată tetrakis, o pavare monoedrică care umple întregul plan euclidian cu triunghiuri dreptunghice isoscele.
Pavarea unei figuri comune cu diverse poliabolouri
modificareProblema compatibilității este să se ia două sau mai multe poliabolouri și să se găsească o figură care poate fi pavată cu oricare dintre poliabolourile luate în considerare. Această problemă a fost studiată mult mai puțin decât problema compatibilității pentru poliominouri. Rezultatele sistematice au apărut pentru prima dată în 2004 pe site-ul Math Magic al lui Erich Friedman.[6]
Note
modificare- ^ en Gardner, Martin (iunie 1967). „The polyhex and the polyabolo, polygonal jigsaw puzzle pieces”. Scientific American. 216 (6): 124–132.
- ^ Șirul A006074 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)
- ^ Șirul A151519 la Enciclopedia electronică a șirurilor de numere întregi (OEIS)
- ^ en Golomb, Solomon W. (). Polyominoes: Puzzles, Patterns, Problems, and Packings (2nd ed.). Princeton University Press. p. 101. ISBN 0-691-02444-8.
- ^ en Goodman, Jacob E.; O'Rourke, Joseph, ed. (). Handbook of Discrete and Computational Geometry (2nd ed.). Chapman & Hall/CRC. p. 349. ISBN 1-58488-301-4.
- ^ en Friedman, Erich. „Polypolyforms”. Math Magic.
Vezi și
modificareLegături externe
modificare- Materiale media legate de poliabolo la Wikimedia Commons
- en Eric W. Weisstein, Polyabolo la MathWorld.
- en Eric W. Weisstein, Triabolo la MathWorld.