Rețea pătrată

Rețele pătrate
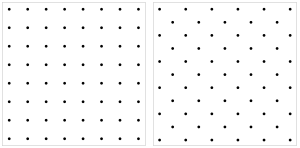
pătrată verticală (simplă)	pătrată diagonală (centrată)

În matematică rețeaua pătrată este un tip de rețea într-un spațiu euclidian bidimensional. Este versiunea bidimensională a rețelelor de întregi, notată prin Z².^[1] Este una dintre cele cinci tipuri de rețele bidimensionale clasificate după grupurile de simetrie;^[2] grupul său de simetrie în notația IUC este p4m^⁠(d),^[3] în notația Coxeter [4,4],^[4] iar în notația orbifold *442.^[5]

Două orientări ale unei imagini a rețelei sunt cele mai comune. Ele pot fi denumite în mod convenabil rețeaua pătrată verticală și rețeaua pătrată diagonală; acesta din urmă se mai numește și rețea pătrată centrată.^[6] Ele diferă de fapt printr-o rotație de 45°. Acest lucru este legat de faptul că o rețea pătrată poate fi împărțită în două subrețele pătrate, așa cum este evident în colorarea unei table de șah.

Simetrie modificare

Categoria simetriei rețelei pătrate este grupul de tapet^⁠(d) p4m. Un model cu această rețea de simetrie de translație nu poate avea mai mult, dar poate avea mai puțină simetrie decât rețeaua în sine. O rețea pătrată verticală poate fi văzută ca o rețea pătrată diagonală cu o dimensiune a ochiurilor de ${\sqrt {2}}$ ori mai mare, având în plus și centrele pătratelor. Analog, după adăugarea centrelor pătratelor la o rețea pătrată verticală se obține o rețea pătrată diagonală cu o dimensiune a ochiului care este de ${\sqrt {2}}$ ori mai mică decât cea a rețelei originale. Un model cu simetrie de rotație cu 4 poziții are o rețea pătrată de centre de rotație cu 4 poziții care este cu un factor de ${\sqrt {2}}$ mai mică și orientată diagonal față de rețeaua cu simetrie de translație.

Cu privire la axele de reflexie, există trei posibilități:

Niciuna. Acesta este grupul de tapet p4.
În patru direcții. Acesta este grupul de tapet p4m.
În două direcții perpendiculare. Acesta este grupul de tapet p4g. Punctele de intersecție ale axelor de reflexie formează o rețea pătrată care este la fel de fină, și orientată la fel cu rețeaua pătrată de centre de rotație cu 4 poziții, cu aceste centre situate în centrele pătratelor formate de axele de reflexie.

p4m, [4,4], (*442)

Grupul de tapet p4, cu aranjarea în interiorul unei celule primitive a centrelor de rotație cu 2 și 4 poziții (aplicabil și pentru p4g și p4m). Un domeniu fundamental este indicat cu galben.	Grupul de tapet p4g. Există axe de reflexie în două direcții, dar nu prin centrele de rotație cu 4 poziții.	Grupul de tapet p4m. Există axe de reflexie în patru direcții, prin centrele de rotație cu 4 poziții. În două direcții axele de reflexie sunt orientate la fel, și la fel de dense ca cele pentru p4g, dar translate. În celelalte două direcții, acestea sunt liniare, de ${\sqrt {2}}$ ori mai dense.

Note modificare

^ en Conway, John; Sloane, Neil J. A. (1999), Sphere Packings, Lattices and Groups, Springer, p. 106, ISBN 9780387985855
^ en Golubitsky, Martin; Stewart, Ian (2003), The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space, Progress in Mathematics, 200, Springer, p. 129, ISBN 9783764321710
^ en Field, Michael; Golubitsky, Martin (2009), Symmetry in Chaos: A Search for Pattern in Mathematics, Art, and Nature (ed. 2nd), SIAM, p. 47, ISBN 9780898717709
^ en Johnson, Norman W.; Weiss, Asia Ivić (1999), „Quadratic integers and Coxeter groups”, Canadian Journal of Mathematics, 51 (6): 1307–1336, doi:10.4153/CJM-1999-060-6 . See in particular the top of p. 1320.
^ en Schattschneider, Doris; Senechal, Marjorie (2004), „Tilings”, În Goodman, Jacob E.; O'Rourke, Joseph, Handbook of Discrete and Computational Geometry, Discrete Mathematics and Its Applications (ed. 2nd), CRC Press, pp. 53–72, ISBN 9781420035315 . See in particular the table on p. 62 relating IUC notation to orbifold notation.
^ en Johnston, Bernard L.; Richman, Fred (1997), Numbers and Symmetry: An Introduction to Algebra, CRC Press, p. 159, ISBN 9780849303012 .

Vezi și modificare

Legături externe modificare

Portal Matematică

Materiale media legate de rețea pătrată la Wikimedia Commons

[1] Conway, John; Sloane, Neil J. A. (1999), Sphere Packings, Lattices and Groups, Springer, p. 106, ISBN 9780387985855

[2] Golubitsky, Martin; Stewart, Ian (2003), The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space, Progress in Mathematics, 200, Springer, p. 129, ISBN 9783764321710

[3] Field, Michael; Golubitsky, Martin (2009), Symmetry in Chaos: A Search for Pattern in Mathematics, Art, and Nature (ed. 2nd), SIAM, p. 47, ISBN 9780898717709

[4] Johnson, Norman W.; Weiss, Asia Ivić (1999), „Quadratic integers and Coxeter groups”, Canadian Journal of Mathematics, 51 (6): 1307–1336, doi:10.4153/CJM-1999-060-6 . See in particular the top of p. 1320.

[5] Schattschneider, Doris; Senechal, Marjorie (2004), „Tilings”, În Goodman, Jacob E.; O'Rourke, Joseph, Handbook of Discrete and Computational Geometry, Discrete Mathematics and Its Applications (ed. 2nd), CRC Press, pp. 53–72, ISBN 9781420035315 . See in particular the table on p. 62 relating IUC notation to orbifold notation.

[6] Johnston, Bernard L.; Richman, Fred (1997), Numbers and Symmetry: An Introduction to Algebra, CRC Press, p. 159, ISBN 9780849303012 .

[1]

[2]

[3]

[4]

[5]

[6]