Caustică (matematică)

Pentru alte sensuri, vedeți Caustică (dezambiguizare).

În geometria diferențială, o caustică este înfășurătoarea^⁠(d) unor drepte, fie reflectate, fie refractate de o varietate (dirimantă). Este legată de conceptul de caustică^⁠(d) din optica geometrică. Sursa razelor poate fi un punct (numit radiant) sau raze paralele dintr-un punct de la infinit, caz în care trebuie specificat un vector de direcție al razelor.

Caustică de reflexie generată de un arc de cerc și un fascicul de raze paralele

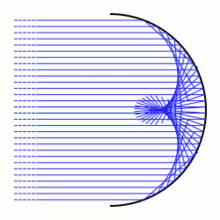
În general, mai ales aplicată la geometria simplectică și teoria singularităților^⁠(d), o caustică este mulțimea valorilor critice ale unei aplicații lagrangiene (π ○ i) : L ↪ M ↠ B; unde i : L ↪ M este o imersiune lagrangiană a unei submulțimi lagrangiene L într-o mulțime simplectică M, iar π : M ↠ B este un fibrat lagrangian al mulțimii simplectice M. Caustica este o submulțime a fibratului lagrangian B.

Explicație

Razele refractate de o suprafață care nu este plană formează caustice unde multe dintre ele se intersectează

Concentrarea luminii, în special a Soarelui, poate arde. Cuvântul caustic provine din greacă καυστός (= fierbinte), prin latină causticus.

O situație comună în care causticele sunt vizibile este la lumina dintr-un pahar de băut. Sticla aruncă o umbră, dar produce și o regiune curbă de lumină strălucitoare. În circumstanțe ideale (inclusiv raze perfect paralele, ca de la o sursă punctuală aflată la infinit), poate fi produsă o zonă de lumină în formă de nefroidă^⁠(d). Causticele ondulate se formează de obicei atunci când lumina strălucește prin valuri de pe apă.

O altă caustică familiară este curcubeul. Împrăștierea luminii prin picăturile de ploaie face ca diferitele lungimi de undă ale luminii să se refracte diferit pe arcele din picături, producând curcubeul.

Catacaustică

O catacaustică este produsă prin reflexie.

Pentru razele care pleacă dintr-un punct radiant, este evoluta podarei radiantului.

Cazul planar cu raze paralele: se presupune că vectorul direcție este $(a,b)$ și curba care reflectă este parametrizată ca $(u(t),v(t))$. Vectorul normal într-un punct este $(-v'(t),u'(t))$; reflectarea vectorului de direcție este (normal necesită o normalizare particulară)

$2{\mbox{proj}}_{n}d-d={\frac {2n}{\sqrt {n\cdot n}}}{\frac {n\cdot d}{\sqrt {n\cdot n}}}-d=2n{\frac {n\cdot d}{n\cdot n}}-d={\frac {(av'^{2}-2bu'v'-au'^{2},bu'^{2}-2au'v'-bv'^{2})}{v'^{2}+u'^{2}}}$

Având componentele vectorului reflectat, el va fi tratat drept tangentă

$(x-u)(bu'^{2}-2au'v'-bv'^{2})=(y-v)(av'^{2}-2bu'v'-au'^{2}).$

Din cea mai simplă formulă a înfășurătoarei se obține

$F(x,y,t)=(x-u)(bu'^{2}-2au'v'-bv'^{2})-(y-v)(av'^{2}-2bu'v'-au'^{2})$

$=x(bu'^{2}-2au'v'-bv'^{2})-y(av'^{2}-2bu'v'-au'^{2})+b(uv'^{2}-uu'^{2}-2vu'v')+a(-vu'^{2}+vv'^{2}+2uu'v')$

$F_{t}(x,y,t)=2x(bu'u''-a(u'v''+u''v')-bv'v'')-2y(av'v''-b(u''v'+u'v'')-au'u'')$

$+b(u'v'^{2}+2uv'v''-u'^{3}-2uu'u''-2u'v'^{2}-2u''vv'-2u'vv'')+a(-v'u'^{2}-2vu'u''+v'^{3}+2vv'v''+2v'u'^{2}+2v''uu'+2v'uu'')$

care poate fi inestetic, dar $F=F_{t}=0$ dă un sistem liniar^⁠(d) în $(x,y)$ și obținerea unei parametrizări a catacausticei este elementară. Se poate folosi regula lui Cramer^⁠(d).

Exemplu

Fie vectorul direcției (0,1) și curba care reflectă $(t,t^{2}).$ Atunci

$u'=1$   $u''=0$   $v'=2t$   $v''=2$   $a=0$   $b=1$

$F(x,y,t)=(x-t)(1-4t^{2})+4t(y-t^{2})=x(1-4t^{2})+4ty-t$

$F_{t}(x,y,t)=-8tx+4y-1$

iar $F=F_{t}=0$ are soluția $(0,1/4).$; De exemplu, lumina care intră întru-n reflector parabolic de-a lungul axei sale este reflectată în focar.

Legături externe

• en Eric W. Weisstein, Caustic la MathWorld.