Dimensiune

În fizică și matematică, dimensiunea unui spațiu (sau obiect) matematic este definită informal ca fiind numărul minim de coordonate necesare pentru a specifica orice punct din interiorul acestuia. Astfel, o linie are dimensiunea unu, deoarece este necesară o singură coordonată pentru a specifica un punct pe ea – de exemplu punctul de la 5 pe o axă a numerelor. O suprafață, cum ar fi un plan, sau suprafața unui cilindru sau a unei sfere, are dimensiunea doi, deoarece sunt necesare două coordonate pentru a specifica un punct pe ea – de exemplu atât latitudinea și longitudinea sunt necesare pentru a găsi un punct pe suprafața unei sfere. Interiorul unui cub, al unui cilindru sau al unei sfere este tridimensional, deoarece sunt necesare trei coordonate pentru a localiza un punct în interiorul acestor spații.

De la stânga la dreapta: pătratul, cubul și tesseractul. Pătratul bidimensional (2D) este mărginit de segmente de dreaptă unidimensionale (1D); cubul tridimensional (3D) prin suprafețe bidimensionale; și tesseractul cvadridimensional (4D) de volume tridimensionale. Pentru afișarea pe o suprafață bidimensională, cum ar fi un ecran, cubul 3D și tesseractul 4D necesită proiecții^⁠(d).

Primele patru dimensiuni spațiale, reprezentate într-o imagine bidimensională.

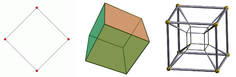
1. Doua puncte pot fi legate pentru a crea un segment.
2. Două segmente de dreaptă paralele pot fi legate pentru a forma un pătrat.
3. Două pătrate paralele pot fi conectate pentru a forma un cub.
4. Două cuburi paralele pot fi conectate pentru a forma un tesseract.

În mecanica clasică, spațiul și timpul sunt categorii diferite și se referă la spațiul și timpul absolute^⁠(d). Această concepție asupra lumii este un spațiu cvadridimensional, dar nu cel care a fost găsit necesar pentru a descrie electromagnetismul. Cele patru dimensiuni ale spațiu-timpului constau în evenimente care nu sunt definite absolut spațial și temporal, ci mai degrabă sunt cunoscute în raport cu mișcarea unui observator^⁠(d). Spațiul Minkowski aproximează mai întâi universul fără gravitație; varietățile pseudo-riemaniene^⁠(d) ale relativității generale descriu spațiu-timpul cu materie și gravitație. Zece dimensiuni sunt folosite pentru a descrie teoria superstringurilor^⁠(d), unsprezece dimensiuni pot descrie supergravitația și teoria M, iar spațiul stărilor mecanicii cuantice este un spațiu funcțional infinit-dimensional.

Conceptul de dimensiune nu se limitează la obiectele fizice. Suprafața spațială mare apare frecvent în matematică și științe. Acestea pot fi spații de parametri^⁠(d) sau de configurație^⁠(d), cum ar fi mecanica lagrangiană sau hamiltoniană; acestea sunt spații abstracte, independente de spațiul fizic în care trăim.

Vezi și

• Dimensiune (matematică)