Rigiditate structurală

În geometria discretă și mecanică rigiditatea structurală este o teorie combinatorică pentru prezicerea flexibilității ansamblurilor formate din corpuri rigide conectate prin legături sau articulații (balamale) flexibile.

Definiții

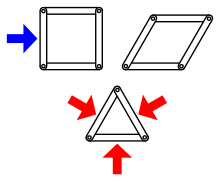
Rigiditatea este proprietatea unei structuri că nu se deformează la aplicarea unei forțe. Opusul rigidității este flexibilitatea. În teoria rigidității structurale, structurile sunt formate din colecții de obiecte care sunt ele însele corpuri rigide, adesea presupuse că iau forme geometrice simple, cum ar fi tije drepte (segmente de dreaptă), cu perechi de obiecte conectate prin articulații flexibile. O structură este rigidă dacă nu se poate flexa; adică dacă nu există o mișcare continuă a structurii în care forma componentelor sale rigide și modelul conexiunilor articulațiilor nu se schimbă.

Există două tipuri diferite de rigiditate. Rigiditatea finită sau rigiditatea macroscopică înseamnă că structura nu se va deforma, nu se va plia sau îndoi relativ mult. Rigiditatea infinitezimală înseamnă că structura nu se va flexa nici măcar prea puțin pentru a fi detectată chiar și în teorie. (Din punct de vedere tehnic, asta înseamnă că anumite ecuații diferențiale nu au soluții nenule.) Importanța rigidității finite este evidentă, dar rigiditatea infinitezimală este, de asemenea, esențială, deoarece flexibilitatea infinitezimală în teorie corespunde flexării minuscule din lumea reală și deteriorării ulterioare a structurii.

Un graf rigid este o încorporare a unui Graf într-un spațiu euclidian care este rigid structural.^[1] Adică un graf este rigid dacă structura formată prin înlocuirea muchiilor cu tije rigide și a nodurilor cu articulații flexibile este rigidă. Un graf care nu este rigid se numește flexibil. Mai formal, o încorporare a unui graf este flexibilă dacă nodurile pot fi mutate continuu, păstrând distanțele dintre nodurile adiacente, cu rezultatul că distanțele dintre unele noduri neadiacente sunt modificate.^[2] Ultima condiție exclude congruențele euclidiene, cum ar fi translația și rotația simplă.

De asemenea, este posibil să se ia în considerare probleme de rigiditate la grafuri în care unele muchii reprezintă elemente de compresiune (care se pot alungi, dar nu și scurta), în timp ce alte muchii reprezintă elemente de întindere (care se pot scurta, dar nu și alungi). Un graf rigid cu muchii de aceste tipuri formează un model matematic al unei structuri de tensegritate^⁠(d).

Matematica rigidității

Problema fundamentală este prezicerea rigidității unei structuri prin analiză teoretică, fără a fi nevoie să fie construită. Rezultatele cheie în acest domeniu cuprind următoarele:

În orice dimensiune, rigiditatea legăturilor de tip tije articulate este descrisă de un matroid^⁠(d). Bazele matroidului de rigiditate^⁠(d) bidimensional (grafuri minime rigide) sunt grafuri Laman^⁠(d).
Teorema lui Cauchy afirmă că un poliedru convex tridimensional cu fețe rigide conectate prin balamale de-a lungul laturilor sale formează o structură rigidă.
Poliedre flexibile. Poliedre neconvexe care nu sunt rigide au fost construite de Raoul Bricard, Robert Connelly și alții. Teorema tare a burdufului afirmă că la orice mișcare continuă a unui poliedru flexibil, acesta își conservă volumul.
În problema contravântuirilor, în care cadrul care urmează să fie rigidizat este o grilă pătrată cu contravântuiri pe diagonale, rigiditatea structurii poate fi analizată prin modelarea acesteia prin conectivitatea unui graf bipartit subiacent.^[3]^[4] Totuși, în ciuda existenței unor teorii matematice considerabile, în multe alte situații simple nu se știe cum să se analizeze matematic rigiditatea unei structuri.

Note

^ en Eric W. Weisstein, Rigid Graph la MathWorld.
^ en Eric W. Weisstein, Flexible Graph la MathWorld.
^ en Baglivo, Jenny A.; Graver, Jack E. (1983), „3.10 Bracing structures”, Incidence and Symmetry in Design and Architecture, Cambridge Urban and Architectural Studies, Cambridge, UK: Cambridge University Press, pp. 76–87, ISBN 9780521297844
^ en Graver, Jack E. (2001), Counting on Frameworks: Mathematics to Aid the Design of Rigid Structures, The Dolciani Mathematical Expositions, 25, Washington, DC: Mathematical Association of America, ISBN 0-88385-331-0, MR 1843781 . See in particular sections 1.2 ("The grid bracing problem", pp. 4–12), 1.5 ("More about the grid problem", pp. 19–22), 2.6 ("The solution to the grid problem", pp. 50–55), and 4.4 ("Tensegrity: tension bracings", particularly pp. 158–161)

Bibliografie

en Alfakih, Abdo Y. (2007), „On dimensional rigidity of bar-and-joint frameworks”, Discrete Applied Mathematics, 155 (10): 1244–1253, doi:10.1016/j.dam.2006.11.011  , MR 2332317
en Connelly, Robert (1980), „The rigidity of certain cabled frameworks and the second-order rigidity of arbitrarily triangulated convex surfaces”, Advances in Mathematics, 37 (3): 272–299, doi:10.1016/0001-8708(80)90037-7  , MR 0591730
en Crapo, Henry (1979), „Structural rigidity”, Structural Topology (1): 26–45, 73, hdl:2099/521  , MR 0621627
en Maxwell, J. C. (1864), „On reciprocal figures and diagrams of forces”, Philosophical Magazine, 4th Series, 27 (182): 250–261, doi:10.1080/14786446408643663
en Rybnikov, Konstantin; Zaslavsky, Thomas (2005), „Criteria for balance in abelian gain graphs, with applications to piecewise-linear geometry”, Discrete and Computational Geometry, 34 (2): 251–268, arXiv:math/0210052  , doi:10.1007/s00454-005-1170-6, MR 2155721
en Whiteley, Walter (1988), „The union of matroids and the rigidity of frameworks”, SIAM Journal on Discrete Mathematics, 1 (2): 237–255, doi:10.1137/0401025, MR 0941354

Portal Matematică

[Ref_-1] Eric W. Weisstein, Rigid Graph la MathWorld.

[2] Eric W. Weisstein, Flexible Graph la MathWorld.

[3] Baglivo, Jenny A.; Graver, Jack E. (1983), „3.10 Bracing structures”, Incidence and Symmetry in Design and Architecture, Cambridge Urban and Architectural Studies, Cambridge, UK: Cambridge University Press, pp. 76–87, ISBN 9780521297844

[4] Graver, Jack E. (2001), Counting on Frameworks: Mathematics to Aid the Design of Rigid Structures, The Dolciani Mathematical Expositions, 25, Washington, DC: Mathematical Association of America, ISBN 0-88385-331-0, MR 1843781 . See in particular sections 1.2 ("The grid bracing problem", pp. 4–12), 1.5 ("More about the grid problem", pp. 19–22), 2.6 ("The solution to the grid problem", pp. 50–55), and 4.4 ("Tensegrity: tension bracings", particularly pp. 158–161)

[1]

[2]

[3]

[4]