Teorema lui Frégier
Teorema lui Frégier a fost demonstrată de matematicianul francez Frégier în anul 1814/1816 și se enunță astfel:
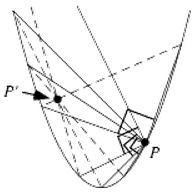
Dreapta care unește punctele unei conice, care dintr-un punct P situat pe conică sunt văzute sub un unghi drept, trece printr-un punct fix P' , situat pe normala la conică în punctul P.
Acest punct se numește punctul lui Frégier și se bucură de mai multe proprietăți. În cazul particular al cercului, punctul lui Frégier se confundă cu centrul, iar în cazul hiperbolei echilatere, acesta este punctul de la infinit al normalei la conică, în punctul dat.
De studiul punctului lui Fregier s-a ocupat și matematicianul român Gheorghe Țițeica în 1915.
Legături externe
modificare- en Wolfram MathWorld: Frégier's Theorem
 | Acest articol referitor la geometrie este deocamdată un ciot. Puteți ajuta wikipedia prin completarea sa! |