Dodecaedru rombohexagonal
| Dodecaedru rombohexagonal | |
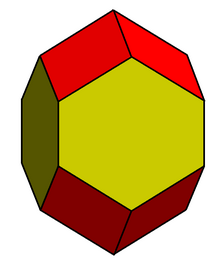 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | paraleloedru |
| Fețe | 12 (8 romburi, 4 hexagoane regulate) |
| Laturi (muchii) | 28 |
| Vârfuri | 18 |
| χ | 2 |
| Configurația vârfului | 8 × 4.6.6 8 × 4.4.6 2 × 4.4.4.4 |
| Grup de simetrie | D4h, [4,2], (*422), ordinul 16 |
| Grup de rotație | D4, [4,2]+, (422), ordinul 8 |
| Proprietăți | convex |
| Desfășurată | |
 | |
În geometrie dodecaedrul rombohexagonal[1] sau dodecaedrul alungit,[2] este un dodecaedru convex cu 8 fețe rombice și 4 fețe hexagonale. Hexagoanele pot fi făcute echilaterale, sau regulate, în funcție de forma romburilor. Poate fi văzut ca fiind construit dintr-un dodecaedru rombic, alungit cu o prismă pătrată.
Alături de dodecaedrul rombic, este un poliedru care umple spațiul, unul dintre cele cinci tipuri de paraleloedre identificate de Evgraf Fiodorov și care umplu spațiul față la față prin translații.
Teselări
modificare- Poate tesela spațiul prin translații.
- Este celula Wigner–Seitz pentru unele rețele cubice centrate intern.
Acestea sunt legate de fagurele dodecaedric rombic cu alungirea zero. Proiectat normal pe direcția de alungire, fagurele arată ca o pavare pătrată cu romburile proiectate în pătrate.
Variații
modificareDodecaedrele rombohexagonale pot fi distorsionate în volume cubice, cu fagurele ca o stivă de cuburi deplasate cu o jumătate de latură. De asemenea, pot fi făcute concave deplasând cele 8 colțuri în jos cu aceeași cantitate cu care centrele sunt deplasate în sus.
| Poliedru coplanar |
Desfășurată |
Fagure |
| Concav |
Desfășurată |
Fagure |
Dodecaedrul rombohexagonal poate fi construit ca o contracție a unui octaedru trunchiat uniform, unde fețele pătrate sunt reduse la laturi, iar fețele hexagonale regulate sunt reduse la fețe rombice cu unghiuri de 60° și 120° (sau perechi de triunghiuri echilaterale). Această construcție alternează pătrate și romburi pe vârfurile cu 4 valențe și are jumătate din simetrie: simetrie D2h, ordinul 8.
| Octaedru trunchiat contractat |
Desfășurată |
Fagure |
Note
modificareBibliografie
modificare- en Robert Williams, The Geometrical Foundation of Natural Structure: A Source Book of Design, Dover Publications Inc., 1979, p. 170, ISBN: 0-486-23729-X
- en H.S.M. Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN: 0-486-61480-8 p. 257