Marele dodecahemidodecaedru

Marele dodecahemidodecaedru
(model 3D)
Descriere
Tip	poliedru uniform neconvex
Fețe	18 (12 pentagrame,         6 decagrame)
Laturi (muchii)	60
Vârfuri	30
χ	−12
Configurația vârfului	5/2.10/3.5/3.10/3
Simbol Wythoff	5/3 5/2 | 5/3 (acoperire dublă)
Grup de simetrie	Ih, [5,3], (*532)
Poliedru dual	marele dodecahemidodecacron
Proprietăți	uniform, neconvex
Figura vârfului

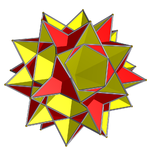
În geometrie marele dodecahemidodecaedru este un poliedru stelat uniform, cu indicele U₇₀. Are 18 fețe (12 pentagrame și 6 decagrame), 60 de laturi și 30 de vârfuri. Un poliedru neconvex are fețe care se intersectează care nu reprezintă laturi sau fețe noi. Doar cele marcate cu sfere aurii sunt vârfuri, iar cele cu linii argintii sunt laturi.

Este un hemipoliedru cu 6 fețe decagramice care trec prin centrul poliedrului. Figura vârfului este un antiparalelogram.

În afară de micul dodecaedru stelat {5/2,5} regulat și marele dodecaedru stelat {5/2,3}, este singurul poliedru uniform neconvex ale cărui fețe sunt toate poligoane regulate neconvexe (poligoane stelate), și anume: pentagrame și decagrame.

Colorarea fețelor sale se poate face în două feluri, în funcție de ce se consideră interior, respectiv exterior al fețelor.

Colorare tradițională

Colorare modulo-2

Mărimi asociate

Coordonate carteziene

Având în comun vârfurile cu icosidodecaedrul, coordonatele carteziene ale vârfurilor marelui dodecahemidodecaedru cu lungimea laturii 2, centrat în origine, sunt toate permutările ale:

$\left(\,0,\,0,\,\pm 2(\varphi -1)\,\right)$

și toate permutările pare ale:

$\left(\,\pm (2-\varphi ),\,\pm (\varphi -1),\,\pm 1,\right)$

unde $\varphi ={\frac {1+{\sqrt {5}}}{2}}$ este secțiunea de aur.

Raza sferei circumscrise

Pentru lungimea laturii egală cu a, raza sferei circumscrise este:

$R=\varphi ^{-1}\,a\approx 0,618034\,a.$

Poliedre înrudite

Anvelopa sa convexă este icosidodecaedrul. Are în comun aranjamentul laturilor cu marele icosidodecaedru (având fețele pentagramice în comun) și cu marele icosihemidodecaedru (având în comun fețele decagramice).

Marele icosicosidodecaedru	Marele dodecahemidodecaedru	Marele icosihemidodecaedru
Icosidodecaedru (anvelopa convexă)

Dual: Marele dodecahemidodecacron

Poliedru dual

Dualul său este marele dodecahemidodecacron.

Vezi și

• Lista poliedrelor uniforme

Legături externe

• en Uniform polyhedra and duals

• en Klitzing, Richard. „3D uniform polyhedra”.  Cheie: gidhid