Prismă hexagonală metabiaugmentată
| Prismă hexagonală metabiaugmentată | |
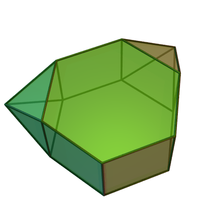 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J55 – J56 – J57 |
| Fețe | 14 (8 triunghiuri echilaterale 4 pătrate; 2 hexagoane)[1] |
| Laturi (muchii) | 26[1] |
| Vârfuri | 14[1] |
| χ | 2 |
| Configurația vârfului | 4 (42.6); 2 (34); 8 (32.4.6) |
| Grup de simetrie | C2v , [2], (*22), ordin 4 |
| Arie | ≈ 12,660 a2 (a = latura) |
| Volum | ≈ 3,069 a3 (a = latura) |
| Poliedru dual | – |
| Proprietăți | convexă |
| Desfășurată | |
 | |
În geometrie prisma hexagonală metabiaugmentată este un poliedru convex construit prin augmentarea unei prisme hexagonale prin atașarea a două piramide pătrate (J1) pe două din fețele sale laterale care nu sunt adiacente sau opuse. Este poliedrul Johnson J56.[1][2] Când două astfel de piramide sunt atașate la fețele laterale opuse, rezultatul este o prismă hexagonală parabiaugmentată (J55). Poliedrul obținut prin atașarea piramidelor la fețele laterale adiacente nu este convex, prin urmare nu este un poliedru Johnson.
Având 14 fețe, este un tetradecaedru.
Mărimi asociate
modificarePentru o prismă hexagonală augmentată cu lungimea laturilor egală cu 2 coordonatele vârfurilor sunt date de:
În acest caz, axa de simetrie a poliedrului va coincide cu axa Oz, iar două plane de simetrie vor coincide cu planele xOz și yOz.
Următoarele formule pentru arie, A și volum, V sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:[1]
Note
modificare- ^ a b c d e en Stephen Wolfram, "Metabiaugmented hexagonal prism" from Wolfram Alpha. Retrieved January 4, 2023.
- ^ en Johnson, Norman W. (), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603