Icositetraedru
poliedru cu 24 de fețe
 Convex, Catalan |
 Convex, Johnson |
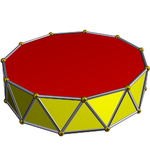 Convex, antiprismă |
 Neconvex, stelat |
În geometrie un icositetraedru[1][2] este un poliedru cu 24 de fețe. Există numeroase forme simetrice, iar unele dintre cele foarte simetrice au simetrie icosaedrică chirală
Exemple de icositetraedre
modificareConvexe
modificareExistă patru poliedre Catalan cu câte 24 de fețe:[3]
| Imagine | Denumire | Tipul fețelor |
|---|---|---|
| Octaedru triakis | triunghiuri isoscele | |
| Hexaedru tetrakis | triunghiuri isoscele | |
| Icositetraedru romboidal | romboizi | |
| Icositetraedru pentagonal | pentagoane neregulate |
Există două poliedre Johnson cu câte 24 de fețe:[4]
| Imagine | Denumire | Tipul fețelor |
|---|---|---|
| Hebesfenmegacoroană | triunghiuri regulate și pătrate | |
| Dodecaedru triaugmentat | triunghiuri regulate și pentagoane |
Alte poliedre convexe
modificare- Prismă icosidigonală (bazele sunt 22-goane)
- Trunchi icosidigonal (bazele sunt 22-goane)
- Antiprismă endecagonală (bazele sunt 11-goane)
- Piramidă icositrigonală (baza este un 23-gon)
- Bipiramidă dodecagonală
- Cupolă endecagonală
Neconvexe
modificareStelate
modificare| Imagine | Denumire | Tipul fețelor |
|---|---|---|
| Micul rombihexacron | patrulater autointersectat | |
| Marele rombihexacron | patrulater autointersectat | |
| Micul icositetraedru hexacronic | patrulater autointersectat | |
| Marele icositetraedru hexacronic | romboizi convecși | |
| Marele icositetraedru romboidal | romboizi concavi | |
| Marele icositetraedru trakis | triunghiuri isoscele |
Note
modificare- ^ „icositetraedru” la DEX online
- ^ en „Greek numerical prefixes”.
- ^ fr Eugène Catalan Mémoire sur la Théorie des Polyèdres. J. l'École Polytechnique (Paris) 41, 1-71, 1865
- ^ en Johnson, Norman W. (). „Convex Solids with Regular Faces”. Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. ISSN 0008-414X. Zbl 0132.14603. Conține enumerarea celor 92 de poliedre și conjectura că nu există altele.