Micul cubicuboctaedru
| Micul cubicuboctaedru | |
 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru uniform neconvex |
| Fețe | 20 (8 triunghiuri, 6 pătrate, 6 octogoane) |
| Laturi (muchii) | 48 |
| Vârfuri | 24 |
| χ | −4 |
| Configurația vârfului | 4.8.3/2.8[1] |
| Simbol Wythoff | 3/2 4 | 4[1] sau 3 4/3 | 4 |
| Diagramă Coxeter | |
| Grup de simetrie | Oh, [4,3], (*432) [1] |
| Grup de rotație | O, [4,3]+, (432) |
| Volum | ≈5,771 a3 (a = latura) |
| Poliedru dual | micul icositetraedru hexacronic |
| Proprietăți | uniform, neconvex |
| Figura vârfului | |
 | |
În geometrie micul cubicuboctaedru este un poliedru stelat uniform, cu indicele U13. Are 20 de fețe (8 triunghiuri, 6 pătrate și 6 octogoane), 48 de laturi și 24 de vârfuri.[1] Fețele pătrate și fețele octogonale sunt paralele cu cele ale unui cub, în timp ce fețele triunghiulare sunt paralele cu cele ale unui octaedru, de unde și numele de cubicuboctaedru. Prefixul mic servește să-l deosebească de marele cubicuboctaedru, care are și el fețele în direcțiile menționate mai sus.[2] Avînd 20 de fețe este un tip de icosaedru.
Este reprezentat prin diagramele Coxeter–Dynkin ![]()
![]()
![]()
![]() . Figura vârfului este un patrulater autointersectat. Un poliedru neconvex are fețe care se intersectează care nu reprezintă laturi sau fețe noi. Doar cele marcate cu sfere aurii sunt vârfuri, iar cele cu linii argintii sunt laturi.
. Figura vârfului este un patrulater autointersectat. Un poliedru neconvex are fețe care se intersectează care nu reprezintă laturi sau fețe noi. Doar cele marcate cu sfere aurii sunt vârfuri, iar cele cu linii argintii sunt laturi.
Are simbolul Wythoff 3/2 4 | 4.[1]
Mărimi asociate modificare
Coordonate carteziene modificare
Având același aranjament al vârfurilor cu rombicuboctaedrul, coordonatele carteziene ale vârfurilor, centrat în origine, cu lungimea laturii de 2, sunt toate permutările ale
Volum modificare
Următoarea formulă pentru volum V este stabilită pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:
Poliedre înrudite modificare
Are în comun aranjamentul vârfurilor cu hexaedrul trunchiat stelat. În plus, are în comun aranjamentul laturilor cu rombicuboctaedrul convex (având 6 fețe pătrate în comun) și cu micul rombihexaedru (având fețele octogonale în comun).
| Rombicuboctaedru |
Micul cubicuboctaedru |
Micul rombihexaedru |
Hexaedrul trunchiat stelat |
Poliedru dual modificare
Dualul său este micul icositetraedru hexacronic.[3]
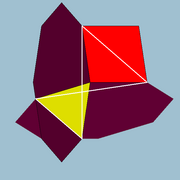
Pavări înrudite modificare
(În această pavare culorile roșu și galben sunt inversate față de colorarea poliedrului.)
După cum sugerează caracteristica Euler, micul cubicuboctaedru este un poliedru toroidal de genul 3 (topologic este o suprafață din genul 3), prin urmare poate fi interpretat ca o imersiune poliedrică(d) a unei suprafețe poliedrice de genul 3, în complementul celor 24 de vârfuri ale sale, în spațiul tridimensional. (O vecinătate a oricărui vârf este din punct de vedere topologic un con pe o 8-figură, care nu poate apărea într-o imersiune. Referința Richter trece cu vederea acest fapt.) Poliedrul subiacent (ignorând autointersectările) definește o pavare uniformă a acestei suprafețe, deci micul cubicuboctaedru este un poliedru uniform. În limbajul politopurilor abstracte, micul cubicuboctaedru este o realizare fidelă a acestui poliedru toroidal abstract, adică este un poliedru nedegenerat, cu același grup de simetrie. De fapt, orice automorfism al suprafeței abstracte de genul 3 cu această pavare este realizat printr-o izometrie a spațiului euclidian.
Suprafețele de genuri superioare (genul 2 sau mai mare) admit o metrică cu curbură constantă negativă (prin teorema de uniformizare(d)), iar acoperirea universală a suprafeței Riemann(d) rezultate este planul hiperbolic. Pavarea corespunzătoare din planul hiperbolic(d) are figura vârfului 3.8.4.8 (triunghi, octogon, pătrat, octogon). Dacă suprafeței i se dă metrica corespunzătoare curburii = −1, acoperirea este o izometrie locală și, prin urmare, figura abstractă a vârfului este aceeași. Această pavare poate fi indicată prin simbolul Wythoff 3 4 | 4.
Alternativ și mai subtil, divizând fiecare față pătrată în 2 triunghiuri și fiecare față octogonală în 6 triunghiuri, micul cubicuboctaedru poate fi interpretat ca o colorare neregulată a pavării combinatoric regulate (nu doar uniforme) a suprafeței de genul 3 cu 56 de triunghiuri echilaterale, care se întâlnesc câte 7 în fiecare din cele 24 de vârfuri.[4] Această pavare regulată este semnificativă, deoarece este o pavare a cuarticei Klein, suprafața de genul 3 cu cea mai simetrică metrică (automorfismele acestei pavări sunt la fel cu izometriile suprafeței) și grupul de automorfism care conservă orientarea acestei suprafețe este izomorf cu grupul liniar special proiectiv(d) PSL(2,7), echivalent cu GL(3,2) (grupul de ordinul 168 al tuturor izometriilor care conservă orientarea). De observat că micul cubicuboctaedrul nu este o realizare a acestui poliedru abstract, deoarece are doar 24 de simetrii care conservă orientarea (nu orice automorfism abstract este realizat printr-o izometrie euclidiană) — izometriile micului cubicuboctaedru conservă nu numai pavarea triunghiulară, ci și colorarea, prin urmare sunt un subgrup propriu al grupului complet de izometrie.
Pavarea corespunzătoare a planului hiperbolic (acoperirea universală) este pavarea triunghiulară de ordinul 7. Grupul de automorfism al cuarticii Klein poate fi mărit (printr-o simetrie care nu se realizează printr-o simetrie a poliedrului, și anume interschimbând cele două capete ale laturilor care divid pătratele și octaedrele) pentru a rezulta grupul Mathieu(d) M24.[5]
Note modificare
- ^ a b c d e en Maeder, Roman. „13: small cubicuboctahedron”. MathConsult. Accesat în .
- ^ en Webb, Robert. „Great Cubicuboctahedron”. Stella: Polyhedron Navigator.
- ^ en Wenninger, Magnus (), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208
- ^ a b Richter, de observat că fiecare față a poliedrului este formată din mai multe fețe în pavare, de unde descrierea drept colorare — două fețe triunghiulare formează o față pătrată etc.
- ^ Richter
Bibliografie modificare
- en Richter, David A., How to Make the Mathieu Group M24, arhivat din original la , accesat în
Vezi și modificare
Legături externe modificare
- en Klitzing, Richard. „3D uniform polyhedra”. Cheie: socco