Funcție
În matematică, o funcție este o relație care asociază fiecărui element dintr-o mulțime (domeniul) un singur element dintr-o altă (posibil din aceeași) mulțime (codomeniul). Noțiunea de funcție este fundamentală în aproape toate ramurile matematicii și în toate științele exacte.
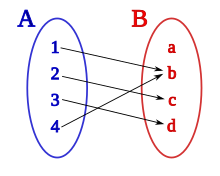
Definiție formală
modificareFie A și B două mulțimi. Se notează cu G produsul lor cartezian: G = A × B.
Fie F o submulțime a lui G.
F este o funcție dacă îndeplinește următoarele două condiții:
- Pentru orice element x din mulțimea A, există un element y în mulțimea B astfel încât perechea (x, y) se află în F.
- Pentru oricare două perechi (x1 , y1) și (x1, y2) din F, y1 = y2.
Funcțiile pot fi definite astfel:
- Prin tabel : f : { 4, 5, 6 } → { 1, 2 } ; f ( 4 ) = 1, f ( 5 ) = 2, f ( 6 ) = 1
- Printr-o expresie algebrică (sau mai multe expresii algebrice diferite pe porțiuni ale domeniului) : f : R → R ; f ( x ) = 3x - 1
Imaginea funcției
modificareImaginea unei funcții este o submulțime a lui B alcătuită din toate valorile . Se notează Im sau .
- Im sau
- Im
Graficul funcției
modificareGraficul funcției Gf=
Proprietăți
modificareInjectivitate
modificareO funcție f:A→B se numește „injectivă” sau „injecție” dacă asociază fiecărui element din domeniu un element diferit din codomeniu. Definiții:
- atunci f(x)≠f(y) sau
- dacă f(x)=f(y) atunci x=y
Interpretare geometrică: O funcție f este injectivă dacă și numai dacă orice paralelă la axa Ox intersectează graficul funcției f în cel mult un punct.
Un exemplu este funcția .
Deoarece pentru x≠y avem x3 ≠ y3, înseamnă că funcția f este injectivă.
Surjectivitate
modificareO funcție f:A→B se numește „surjectivă” sau „surjecție” dacă asociază fiecărui element din codomeniu un element din domeniu. Respectiv, , atunci astfel încât f(x)=y.
Interpretare geometrică: O funcție f este surjectivă dacă orice paralelă la Ox printr-un punct de pe Oy intersectează graficul funcției f în cel puțin un punct.
O funcție surjectivă, de exemplu, este , f(x)=|x|, atunci astfel încât f(y)=f(-y).
Bijectivitate
modificareO funcție f:A→B se numește „bijectivă” sau „bijecție” dacă este și injectivă și surjectivă. Respectiv, f este o bijecție dacă , unic astfel încât f(x)=y.
Interpretare geometrică: O funcție f este bijectivă dacă și numai dacă orice paralelă la axa Ox printr-un punct de pe Oy intersectează graficul funcției f în exact un punct.
Un exemplu de funcție bijectivă este , f(x)=x+3, atunci astfel încât f(x)=y, iar acel x este y-3, unic.
Inversa unei funcții
modificareO funcție se numește „inversabilă” dacă și numai dacă există funcția astfel încât . Atunci se numește „inversa” funcției și se notează . Funcția este inversabilă dacă și numai dacă este bijectivă.
- Inversa unei funcții este unică și simetrică față de funcție.
- Graficele funcțiilor numerice și sunt simetrice față de prima bisectoare, dreapta cu ecuația .
Paritatea funcției
modificareO funcție cu valori reale, unde , se numește „pară” dacă . Graficul unei funcții pare este simetric față de axa Oy.
O funcție cu valori reale se numește „impară” dacă
- sau
- .
Graficul unei funcții impare este simetric față de origine.
Proprietăți
modificare- Singura funcție care este și pară și impară este funcția constantă egală cu zero.
- Suma și diferența a două funcții de aceeași paritate mențin acea paritate.
- Orice multiplu al unei funcții are aceeași paritate ca funcția originală.
- Produsul a două funcții de aceeași paritate este o funcție pară.
- Produsul unei funcții pare cu o funcție impară este o funcție impară.
- Raportul dintre două funcții de aceeași paritate este o funcție pară.
- Raportul dintre o funcție pară cu o funcție impară este o funcție impară.
Monotonie
modificareLegături externe
modificare- The Wolfram Functions Site gives formulae and visualizations of many mathematical functions.
- Shodor: Function Flyer, interactive Java applet for graphing and exploring functions.
- xFunctions, a Java applet for exploring functions graphically.
- Draw Function Graphs, online drawing program for mathematical functions.
- Functions from cut-the-knot.
- Function at ProvenMath.
- Comprehensive web-based function graphing & evaluation tool Arhivat în , la Wayback Machine..
- FunctionGame, an educational interactive function guessing games.

