Utilizator:Jobava-ro/ciorne/Orbită


În fizică, o orbită este traiectoria urmată de un corp în jurul altui corp sub efectul gravitației. De exemplu, orbita unei planete în jurul baricentrului unui sistem solar.[1][2] Orbitele planetelor sunt de regulă eliptice, unde steaua sau baricentrul ocupă unul dintre focarele elipsei.
Cea mai precisă teorie a dinamicii orbitale este dată de teoria generală a relativității, de Albert Einstein, care consideră gravitația ca rezultat al curburii spațiu-timpului, iar orbitele ca „geodezice” (linii care urmează cea mai scurtă distanță) în acest spațiu curbat. Pentru ușurința calculelor, se folosesc în practică teoria gravitației universale a lui Newton, bazată pe legile lui Kepler de dinamică planetară.[3]
Istorie
modificareDin punct de vedere istoric, mișcarea aparentă a planetelor a fost pentru prima data înțeleasă geometric sub formă de epicicle, dinamică realizată din mișcarea unor „cercuri în cercuri”, adică suma a numeroase mișcări circulare.[4] Aceste teorii puteau prezice mișcarea planetelor cu un nivel rezonabil de precizie, pentru acele vremuri, până când Johannes Kepler a dovedit că mișcarea planetelor urmează de fapt traiectoria unor elipse, model matematic mult mai simplu și precis.[5]
În modelul geocentric al sistemului solar se explică mișcarea aparentă a planetelor pe fundalul stelelor fixe folosind ideea de sfere cerești. Planetele ar fi fixate pe o serie de sfere transparente concentrice aflate mișcare, în timp ce stelele se află fixate pe o altă sferă exterioară, fixă. Dar după măsurarea mai precisă a mișcărilor aparente ale planetelor, au fost create mecanisme teoretice care folosesc ideea de epiciclu și deferent. Deși modelul matematic producea rezultate rezonabile, pentru creșterea preciziei trebuiau adăugate tot mai multe epicicluri, care făceau calculul foarte complicat.
Baza teoriei moderne a orbitelor a fost formulată de Johannes Kepler prin cele trei legi de mișcare planetară ale sale. Mai întâi Kepler a descoperit că orbitele planetelor din Sistemul Solar sunt eliptice și nu circulare (sau epiciclice) și că Soarele nu se găsește la centrul elipsei, ci la unul din focare.[6] Apoi, a descoperit că viteza planetelor nu este constantă, cum s-a crezut, ci variază în funcție de distanța față de Soare. În ultimul rând, a descoperit că, pentru planete, cubul distanței lor față de Soare este proporțional cu pătratul perioadelor orbitale. Jupiter și Venus, de exemplu, se găsesc la 5,2 și 0,723 u.a. de Soare iar perioadele orbitale sunt de 11,86 și 0,615 ani, respectiv. Se poate observa proporționalitatea pentru Jupiter și Venus: 5,23/11,862 ≈ 0.7233/0.6152 ≈ 1.
Isaac Newton a demonstrat că legile lui Kepler sunt derivabile din teoria sa a gravitației universale și că, în general, traiectoriile corpurilor sub acțiunea gravitației unui singur punct sunt secțiuni conice (dacă forța gravitațională se propagă instantaneu). Newton a arătat că, pentru doar două corpuri sub acțiune reciprocă, mărimea orbitelor lor este invers proporțională cu masa și că acele corpuri orbitează baricentrul sistemului. Atunci când unul dintre corpuri este mult mai masiv, este rezonabil să considerăm corpul mai masiv ca nefiind în mișcare și ca focar al orbitei.
Albert Einstein a arătat că gravitația se datorează curburii spațiu-timpului, și s-a eliminat cerința ca gravitația să se propage instantaneu. În relativism, orbitele urmează traiectorii (geodezice) aproximate foarte bine de legile lui Newton, cu excepția câmpurilor gravitaționale foarte puternice sau a vitezelor foarte mari. Primul calcul al unei distorsionări relativiste s-a realizat din analiza mișcării planetei Mercur, raportat la intensitatea locală a câmpului gravitațional solar, care induc o ușoară precesie orbitei efective a lui Mercur.
Totuși, teoria lui Newton este încă folosită în practică pentru că oferă un nivel rezonabil de precizie și este mult mai ușor de folosit.
Orbite planetare
modificareÎntr-un sistem planetar, planetele, planetele pitice, asteroizii și alte planete minore, precum și gunoiul orbital orbitează baricentrul unui sistem în cazul orbitelor eliptice. O cometă aflată pe o traiectorie parabolică sau hiperbolică părăsește influența gravitațională a stelei și nu este considerată parte a sistemului planetar. Corpuri legate gravitațional de una dintre planete, sateliți naturali sau artificiali, orbitează în jurul unui baricentru din apropierea sau din interiorul planetei.
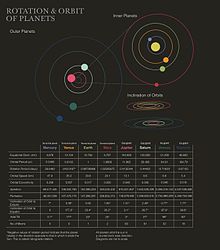
Ca urmare a perturbărilor gravitaționale, excentricitățile orbitelor planetare variază în timp. Mercur, cea mai mică planetă din Sistemul Solar, are cea mai excentrică orbită. În epoca curentă, Marte are a doua cea mai mare excentricitate, în timp ce Venus și Neptun au cele mai mici valori.
Periapsa este punctul de apropiere minim dintre două corpuri care se orbitează reciproc și apoapsa este punctul de maximă separație. (Pot exista termeni mai specifici pentru anumite corpuri. De exemplu, perigeu și apogeu pentru apropierea minimă, respectiv maximă față de Pământ a unui corp care orbitează sau periheliu și afeliu pentru un corp care orbitează Soarele.)
În cadrul orbitelor eliptice multiple, baricentrul se află într-unul dintre focarele tuturor orbitelor (cu nimic altceva la celălalt focar). Pe măsură ce o planetă se apropie de periapsă, viteza acesteia va crește și apoi va descrește pe măsură ce se apropie de apoapsă.
Teorii ale orbitelor
modificareOrbitele pot fi înțelese în mai multe feluri:
- Suprafața unui corp se curbează sub obiectul care „cade” înspre acesta în mod egal cu căderea în așa fel încât corpul nu atinge niciodată suprafața
- Gravitația curbează traiectoria rectilinie a unui corp cu masă.
- Un corp care se mișcă tangențial „cade” spre un corp central, dar are suficientă viteză tangențială pentru a nu se intersecta cu corpul central și va continua să cadă o perioadă nedeterminată.
Pentru ilustrarea unei orbite în jurul unei planete se poate folosi metafora ghiuleaua lui Newton. Este un „experiment mental” în care un tun amplasat pe un munte înalt poate propulsa o ghiulea pe un plan orizontal și cu posibilitatea de a varia viteza ghiulelei de pe țeava tunului. Se ignoră efectele frecării cu aerul, sau se consideră muntele suficient de înalt pentru o atmosferă suficient de rarefiată.[7]
Dacă tunul propulsează ghiuleaua cu o viteză mică inițială, traiectoria ghiulelei se va curba și va lovi pământul (A). Dacă se crește viteza de propulsie, ghiuleaua va lovi pământul la o distanță mai mare (B). Iar dacă se crește și mai mult viteza (C) și (D) atunc ghiuleaua va reveni la punctul inițial pe o traiectorie curbată și nu se va intersecta cu pământul. Toate aceste traiectorii sunt „orbite” în jurul centrului Pământului, doar că se intersectează cu suprafața Pământului.
Pentru fiecare combinație de înălțime deasupra centrului de masă a planetei există o viteză la care se poate menține o orbită care nu se intersectează cu suprafața, care produce o orbită circulară (C).
Pe măsură ce crește viteza ghiulelei, se produce o orbită eliptică (D). Conform diagramei, distanța cea mai mare față de Pământ se petrece în punctul opus (trasat prin centrul Pământului) al orbitei, adică jumătatea perimetrului orbitei și distanță minimă este chiar punctul de tragere. Tot conform diagramei, orbita fiind o elipsă, ghiuleaua riscă să lovească tunul din spate dacă acesta nu e mutat.
La o viteză specifică, numită „viteză de eliberare”, ghiuleaua va descrie o traiectorie parabolică și nu va reveni niciodată înapoi. Dacă se crește viteza și mai mult, traiectoria va fi hiperbolică.
Relația dintre două mase în mișcare poate fi descrisă în 4 cazuri:
- Fără orbite
- Traiectorii suborbitale
- Traiectorii eliptice întrerupte
- Traiectorii orbitale (sau „orbite”)
- Range of elliptical paths with closest point opposite firing point
- Circular path
- Range of elliptical paths with closest point at firing point
- Traiectorii deschise („de eliberare”)
- Traiectorii parabolice
- Traiectorii hiperbolice
În practică, rachetele lansate de pe suprafața Pământului au la început o traiectorie verticală pentru a putea ieși din atmosferă, apoi traiectoria se înclină și vectorul propulsiei devine paralel Pământul pentru o eficiență maximă. Dacă o orbită eliptică se intersectează cu atmosfera, obiectul orbital va pierde din viteză și dacă pierde prea mult poate reintra și cădea înapoi pe suprafața Pământului. Această manevră se mai numește și aerofrânare (sau aerocaptură) și este folosită de unele vehicule spațiale pentru a economisi combustibil pentru frânare și pentru a intra în orbita unor corpuri cerești cu atmosferă.
Legile lui Newton
modificareTeoria lui Newton pentru două corpuri
modificareIn many situations relativistic effects can be neglected, and Newton's laws give a highly accurate description of the motion. The acceleration of each body is equal to the sum of the gravitational forces on it, divided by its mass, and the gravitational force between each pair of bodies is proportional to the product of their masses and decreases inversely with the square of the distance between them. To this Newtonian approximation, for a system of two point masses or spherical bodies, only influenced by their mutual gravitation (the two-body problem), the orbits can be exactly calculated. If the heavier body is much more massive than the smaller, as for a satellite or small moon orbiting a planet or for the Earth orbiting the Sun, it is accurate and convenient to describe the motion in a coordinate system that is centered on the heavier body, and we say that the lighter body is in orbit around the heavier. For the case where the masses of two bodies are comparable, an exact Newtonian solution is still available, and qualitatively similar to the case of dissimilar masses, by centering the coordinate system on the center of mass of the two.
Definirea energiei potențiale gravitaționale
modificareEnergy is associated with gravitational fields. A stationary body far from another can do external work if it is pulled towards it, and therefore has gravitational potential energy. Since work is required to separate two bodies against the pull of gravity, their gravitational potential energy increases as they are separated, and decreases as they approach one another. For point masses the gravitational energy decreases without limit as they approach zero separation, and it is convenient and conventional to take the potential energy as zero when they are an infinite distance apart, and then negative (since it decreases from zero) for smaller finite distances.
Energii orbitale și formele orbitelor
modificareWith two bodies, an orbit is a conic section. The orbit can be open (so the object never returns) or closed (returning), depending on the total energy (kinetic + potential energy) of the system. In the case of an open orbit, the speed at any position of the orbit is at least the escape velocity for that position, in the case of a closed orbit, always less. Since the kinetic energy is never negative, if the common convention is adopted of taking the potential energy as zero at infinite separation, the bound orbits have negative total energy, parabolic trajectories have zero total energy, and hyperbolic orbits have positive total energy.
An open orbit has the shape of a hyperbola (when the velocity is greater than the escape velocity), or a parabola (when the velocity is exactly the escape velocity). The bodies approach each other for a while, curve around each other around the time of their closest approach, and then separate again forever. This may be the case with some comets if they come from outside the solar system.
A closed orbit has the shape of an ellipse. In the special case that the orbiting body is always the same distance from the center, it is also the shape of a circle. Otherwise, the point where the orbiting body is closest to Earth is the perigee, called periapsis (less properly, "perifocus" or "pericentron") when the orbit is around a body other than Earth. The point where the satellite is farthest from Earth is called apogee, apoapsis, or sometimes apifocus or apocentron. A line drawn from periapsis to apoapsis is the line-of-apsides. This is the major axis of the ellipse, the line through its longest part.
Legile lui Kepler
modificareOrbiting bodies in closed orbits repeat their paths after a constant period of time. This motion is described by the empirical laws of Kepler, which can be mathematically derived from Newton's laws. These can be formulated as follows:
- The orbit of a planet around the Sun is an ellipse, with the Sun in one of the focal points of the ellipse. [This focal point is actually the barycenter of the Sun-planet system; for simplicity this explanation assumes the Sun's mass is infinitely larger than that planet's.] The orbit lies in a plane, called the orbital plane. The point on the orbit closest to the attracting body is the periapsis. The point farthest from the attracting body is called the apoapsis. There are also specific terms for orbits around particular bodies; things orbiting the Sun have a perihelion and aphelion, things orbiting the Earth have a perigee and apogee, and things orbiting the Moon have a perilune and apolune (or periselene and aposelene respectively). An orbit around any star, not just the Sun, has a periastron and an apastron.
- As the planet moves around its orbit during a fixed amount of time, the line from the Sun to planet sweeps a constant area of the orbital plane, regardless of which part of its orbit the planet traces during that period of time. This means that the planet moves faster near its perihelion than near its aphelion, because at the smaller distance it needs to trace a greater arc to cover the same area. This law is usually stated as "equal areas in equal time."
- For a given orbit, the ratio of the cube of its semi-major axis to the square of its period is constant.
Limite ale legilor lui Newton
modificareNote that while bound orbits around a point mass or around a spherical body with a Newtonian gravitational field are closed ellipses, which repeat the same path exactly and indefinitely, any non-spherical or non-Newtonian effects (as caused, for example, by the slight oblateness of the Earth, or by relativistic effects, changing the gravitational field's behavior with distance) will cause the orbit's shape to depart from the closed ellipses characteristic of Newtonian two-body motion. The two-body solutions were published by Newton in Principia in 1687. In 1912, Karl Fritiof Sundman developed a converging infinite series that solves the three-body problem; however, it converges too slowly to be of much use. Except for special cases like the Lagrangian points, no method is known to solve the equations of motion for a system with four or more bodies.
Abordări în problemele cu mai multe corpuri
modificareInstead, orbits with many bodies can be approximated with arbitrarily high accuracy. These approximations take two forms:
- One form takes the pure elliptic motion as a basis, and adds perturbation terms to account for the gravitational influence of multiple bodies. This is convenient for calculating the positions of astronomical bodies. The equations of motion of the moons, planets and other bodies are known with great accuracy, and are used to generate tables for celestial navigation. Still, there are secular phenomena that have to be dealt with by post-Newtonian methods.
- The differential equation form is used for scientific or mission-planning purposes. According to Newton's laws, the sum of all the forces will equal the mass times its acceleration (F = ma). Therefore accelerations can be expressed in terms of positions. The perturbation terms are much easier to describe in this form. Predicting subsequent positions and velocities from initial values corresponds to solving an initial value problem. Numerical methods calculate the positions and velocities of the objects a short time in the future, then repeat the calculation. However, tiny arithmetic errors from the limited accuracy of a computer's math are cumulative, which limits the accuracy of this approach.
Differential simulations with large numbers of objects perform the calculations in a hierarchical pairwise fashion between centers of mass. Using this scheme, galaxies, star clusters and other large objects have been simulated.[citation needed]
Analiza lui Newton a mișcării orbitale
modificare- (See also Kepler orbit, orbit equation and Kepler's first law.)
The earth follows an ellipse round the sun. But unlike the ellipse followed by a pendulum or an object attached to a spring, the sun is at a focal point of the ellipse and not at its centre.
The following derives mathematically this orbit as Newton would have done. We start only with the Newtonian law that the gravitational acceleration towards the central body is related to the inverse of the square of the distance between them.
where is the standard gravitational parameter, in this case . We assume that the central body is heavy enough that it can be considered to be stationary and we ignore the more subtle effects of general relativity.
When a pendulum or an object attached to a spring swings in an ellipse, the inward acceleration/force is proportionate to the distance Due to the way vectors add, the component of the force in the or in the directions are also proportionate to the respective components of the distances, . Hence, the entire analysis can be done separately in these dimensions. This results in the harmonic parabolic equations and of the ellipse. But with the decreasing relationship , the dimensions cannot be separated.
The reason that the sun is at the focal point of the orbit's ellipse and not at the centre is because if the object is moving really fast then, as it moves out, the gravitational pull decreases allowing the object to almost escape. If it does not quite escape, then its orbit cycles around first as a parabola. But then when quite far away, it slowly circles back. It picks up speed as it falls, only to boomerang back out into space again.
The location of the orbiting object at the current time is located in the plane using Vector calculus in polar coordinates both with the standard Euclidean basis and with the polar basis with the origin coinciding with the center of force. Let be the distance between the object and the center and be the angle it has rotated. Let and be the standard Euclidean bases and let and be the radial and transverse polar basis with the first being the unit vector pointing from the central body to the current location of the orbiting object and the second being the orthogonal unit vector pointing in the direction that the orbiting object would travel if orbiting in a counter clockwise circle. Then the vector to the orbiting object is
We use and to denote the standard derivatives of how this distance and angle change over time. But we also take the derivative of a vector to see how it changes over time by subtracting its location at time from that at time and dividing by . The result is also a vector. Because our basis vector moves as the object orbits, we start by differentiating it. From time to , the vector keeps its beginning at the origin and rotates from angle to which moves its head a distance in the perpendicular direction giving a derivative of .
We can now find the velocity and acceleration of our orbiting object.
The coefficients of and are the radial and transverse components of the acceleration. As said, Newton gives that this first due to gravity is and the second is zero.
Equation (2) can be rearranged using integration by parts.
We can divide through by because it is not zero unless the orbiting object crashes. Then having the derivative be zero gives that the function is a constant.
which is actually the theoretical proof of Kepler's second law (A line joining a planet and the Sun sweeps out equal areas during equal intervals of time). The constant of integration, h, is the angular momentum per unit mass.
In order to get an equation for the orbit from equation (1), we need to eliminate time.[8] (See also Binet equation.) In polar coordinates, this would express the distance of the orbiting object from the center as a function of its angle . However, it is easier to introduced the auxiliary variable and to express as a function of . Derivatives of with respect to time may be rewritten as derivatives of with respect to angle.
- (reworking (3))
So for the gravitational force – or, more generally, for any inverse square force law – the right hand side of the equation becomes a constant and the equation is seen to be the harmonic equation (up to a shift of origin of the dependent variable). The solution is:
where A and θ0 are arbitrary constants. This resulting equation of the orbit of the object is that of an ellipse in Polar form relative to one of the focal points. This is put into a more standard form by letting be the eccentricity, letting be the semi-major axis. Finally, letting so the long axis of the elipce is along the positive x coordinate.
Mișcare orbitală relativistă
modificareThe above classical (Newtonian) analysis of orbital mechanics assumes that the more subtle effects of general relativity, such as frame dragging and gravitational time dilation are negligible. Relativistic effects cease to be negligible when near very massive bodies (as with the precession of Mercury's orbit about the Sun), or when extreme precision is needed (as with calculations of the orbital elements and time signal references for GPS satellites.[9])
Planuri orbitale
modificareThe analysis so far has been two dimensional; it turns out that an unperturbed orbit is two-dimensional in a plane fixed in space, and thus the extension to three dimensions requires simply rotating the two-dimensional plane into the required angle relative to the poles of the planetary body involved.
The rotation to do this in three dimensions requires three numbers to uniquely determine; traditionally these are expressed as three angles.
Perioadă orbitală
modificareThe orbital period is simply how long an orbiting body takes to complete one orbit.
Specificarea orbitelor
modificareSix parameters are required to specify a Keplerian orbit about a body. For example, the three numbers that specify the body's initial position, and the three values that specify its velocity will define a unique orbit that can be calculated forwards (or backwards). However, traditionally the parameters used are slightly different.
The traditionally used set of orbital elements is called the set of Keplerian elements, after Johannes Kepler and his laws. The Keplerian elements are six:
- Inclination (i)
- Longitude of the ascending node (Ω)
- Argument of periapsis (ω)
- Eccentricity (e)
- Semimajor axis (a)
- Mean anomaly at epoch (M0).
In principle once the orbital elements are known for a body, its position can be calculated forward and backwards indefinitely in time. However, in practice, orbits are affected or perturbed, by other forces than simple gravity from an assumed point source (see the next section), and thus the orbital elements change over time.
Perturbații orbitale
modificareAn orbital perturbation is when a force or impulse which is much smaller than the overall force or average impulse of the main gravitating body and which is external to the two orbiting bodies causes an acceleration, which changes the parameters of the orbit over time.
Perturbații radiale, prograde și transversale
modificareA small radial impulse given to a body in orbit changes the eccentricity, but not the orbital period (to first order). A prograde or retrograde impulse (i.e. an impulse applied along the orbital motion) changes both the eccentricity and the orbital period. Notably, a prograde impulse at periapsis raises the altitude at apoapsis, and vice versa, and a retrograde impulse does the opposite. A transverse impulse (out of the orbital plane) causes rotation of the orbital plane without changing the period or eccentricity. In all instances, a closed orbit will still intersect the perturbation point.
Dezintegrarea orbitelor
modificareIf an orbit is about a planetary body with significant atmosphere, its orbit can decay because of drag. Particularly at each periapsis, the object experiences atmospheric drag, losing energy. Each time, the orbit grows less eccentric (more circular) because the object loses kinetic energy precisely when that energy is at its maximum. This is similar to the effect of slowing a pendulum at its lowest point; the highest point of the pendulum's swing becomes lower. With each successive slowing more of the orbit's path is affected by the atmosphere and the effect becomes more pronounced. Eventually, the effect becomes so great that the maximum kinetic energy is not enough to return the orbit above the limits of the atmospheric drag effect. When this happens the body will rapidly spiral down and intersect the central body.
The bounds of an atmosphere vary wildly. During a solar maximum, the Earth's atmosphere causes drag up to a hundred kilometres higher than during a solar minimum.
Some satellites with long conductive tethers can also experience orbital decay because of electromagnetic drag from the Earth's magnetic field. As the wire cuts the magnetic field it acts as a generator, moving electrons from one end to the other. The orbital energy is converted to heat in the wire.
Orbits can be artificially influenced through the use of rocket engines which change the kinetic energy of the body at some point in its path. This is the conversion of chemical or electrical energy to kinetic energy. In this way changes in the orbit shape or orientation can be facilitated.
Another method of artificially influencing an orbit is through the use of solar sails or magnetic sails. These forms of propulsion require no propellant or energy input other than that of the Sun, and so can be used indefinitely. See statite for one such proposed use.
Orbital decay can occur due to tidal forces for objects below the synchronous orbit for the body they're orbiting. The gravity of the orbiting object raises tidal bulges in the primary, and since below the synchronous orbit the orbiting object is moving faster than the body's surface the bulges lag a short angle behind it. The gravity of the bulges is slightly off of the primary-satellite axis and thus has a component along the satellite's motion. The near bulge slows the object more than the far bulge speeds it up, and as a result the orbit decays. Conversely, the gravity of the satellite on the bulges applies torque on the primary and speeds up its rotation. Artificial satellites are too small to have an appreciable tidal effect on the planets they orbit, but several moons in the solar system are undergoing orbital decay by this mechanism. Mars' innermost moon Phobos is a prime example, and is expected to either impact Mars' surface or break up into a ring within 50 million years.
Orbits can decay via the emission of gravitational waves. This mechanism is extremely weak for most stellar objects, only becoming significant in cases where there is a combination of extreme mass and extreme acceleration, such as with black holes or neutron stars that are orbiting each other closely.
Platitudine
modificareThe standard analysis of orbiting bodies assumes that all bodies consist of uniform spheres, or more generally, concentric shells each of uniform density. It can be shown that such bodies are gravitationally equivalent to point sources.
However, in the real world, many bodies rotate, and this introduces oblateness and distorts the gravity field, and gives a quadrupole moment to the gravitational field which is significant at distances comparable to the radius of the body.
Mai multe corpuri gravitaționale
modificareThe effects of other gravitating bodies can be significant. For example, the orbit of the Moon cannot be accurately described without allowing for the action of the Sun's gravity as well as the Earth's. One approximate result is that bodies will usually have reasonably stable orbits around a heavier planet or moon, in spite of these perturbations, provided they are orbiting well within the heavier body's Hill sphere.
When there are more than two gravitating bodies it is referred to as an n-body problem. Most n-body problems have no closed form solution, although some special cases have been formulated.
Radiația solară și vântul stelar
modificareFor smaller bodies particularly, light and stellar wind can cause significant perturbations to the attitude and direction of motion of the body, and over time can be significant. Of the planetary bodies, the motion of asteroids is particularly affected over large periods when the asteroids are rotating relative to the Sun.
Astrodinamică
modificareOrbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It is a core discipline within space mission design and control. Celestial mechanics treats more broadly the orbital dynamics of systems under the influence of gravity, including spacecraft and natural astronomical bodies such as star systems, planets, moons, and comets. Orbital mechanics focuses on spacecraft trajectories, including orbital maneuvers, orbit plane changes, and interplanetary transfers, and is used by mission planners to predict the results of propulsive maneuvers. General relativity is a more exact theory than Newton's laws for calculating orbits, and is sometimes necessary for greater accuracy or in high-gravity situations (such as orbits close to the Sun).
Orbite în jurul Pământului
modificare- Low Earth orbit (LEO): Geocentric orbits with altitudes up to 2,000 km (0–1,240 miles).[10]
- Medium Earth orbit (MEO): Geocentric orbits ranging in altitude from 2,000 km (1,240 miles) to just below geosynchronous orbit at 35.786 kilometeri (22.236 mi). Also known as an intermediate circular orbit. These are "most commonly at 20.200 kilometeri (12.600 mi), or 20.650 kilometeri (12.830 mi), with an orbital period of 12 hours."[11]
- Both Geosynchronous orbit (GSO) and Geostationary orbit (GEO) are orbits around Earth matching Earth's sidereal rotation period. All geosynchronous and geostationary orbits have a semi-major axis of 42.164 km (26.199 mi).[12] All geostationary orbits are also geosynchronous, but not all geosynchronous orbits are geostationary. A geostationary orbit stays exactly above the equator, whereas a geosynchronous orbit may swing north and south to cover more of the Earth's surface. Both complete one full orbit of Earth per sidereal day (relative to the stars, not the Sun).
- High Earth orbit: Geocentric orbits above the altitude of geosynchronous orbit 35,786 km (22,240 miles).[11]
Constante de proporționalitate
modificareThe gravitational constant G has been calculated as:
- (6.6742 ± 0.001) × 10−11 (kg/m3)−1s−2.
Thus the constant has dimension density−1 time−2. This corresponds to the following properties.
Scaling of distances (including sizes of bodies, while keeping the densities the same) gives similar orbits without scaling the time: if for example distances are halved, masses are divided by 8, gravitational forces by 16 and gravitational accelerations by 2. Hence velocities are halved and orbital periods remain the same. Similarly, when an object is dropped from a tower, the time it takes to fall to the ground remains the same with a scale model of the tower on a scale model of the Earth.
Scaling of distances while keeping the masses the same (in the case of point masses, or by reducing the densities) gives similar orbits; if distances are multiplied by 4, gravitational forces and accelerations are divided by 16, velocities are halved and orbital periods are multiplied by 8.
When all densities are multiplied by 4, orbits are the same; gravitational forces are multiplied by 16 and accelerations by 4, velocities are doubled and orbital periods are halved.
When all densities are multiplied by 4, and all sizes are halved, orbits are similar; masses are divided by 2, gravitational forces are the same, gravitational accelerations are doubled. Hence velocities are the same and orbital periods are halved.
In all these cases of scaling. if densities are multiplied by 4, times are halved; if velocities are doubled, forces are multiplied by 16.
These properties are illustrated in the formula (derived from the formula for the orbital period)
for an elliptical orbit with semi-major axis a, of a small body around a spherical body with radius r and average density σ, where T is the orbital period. See also Kepler's Third Law.
Brevete
modificareAnumite orbite și manevre orbitale au devenit subiectul brevetelor de invenție.[13]
Vezi și
modificareReferințe
modificare- ^ The Space Place :: What's a Barycenter
- ^ orbit (astronomy) – Britannica Online Encyclopedia
- ^ Kuhn, The Copernican Revolution, pp. 238, 246–252
- ^ Encyclopaedia Britannica, 1968, vol. 2, p. 645
- ^ M Caspar, Kepler (1959, Abelard-Schuman), at pp.131–140; A Koyré, The Astronomical Revolution: Copernicus, Kepler, Borelli (1973, Methuen), pp. 277–279
- ^ Jones, Andrew. „Kepler's Laws of Planetary Motion”. about.com. Accesat în .
- ^ See pages 6 to 8 in Newton's "Treatise of the System of the World" (written 1685, translated into English 1728, see Newton's 'Principia' – A preliminary version), for the original version of this 'cannonball' thought-experiment.
- ^ Fitzpatrick, Richard (). „Planetary orbits”. Classical Mechanics – an introductory course. The University of Texas at Austin. Arhivat din original la . Accesat în .
- ^ Pogge, Richard W.; “Real-World Relativity: The GPS Navigation System”.
- ^ „NASA Safety Standard 1740.14, Guidelines and Assessment Procedures for Limiting Orbital Debris” (PDF). Office of Safety and Mission Assurance. .
- ^ a b „Orbit: Definition”. Ancillary Description Writer's Guide, 2013. National Aeronautics and Space Administration (NASA) Global Change Master Directory. Accesat în .
- ^ Vallado, David A. (). Fundamentals of Astrodynamics and Applications. Hawthorne, CA: Microcosm Press. p. 31.
- ^ http://motherboard.vice.com/read/how-satellite-companies-patent-their-orbits
Bibliografie
modificare- Abell; Morrison; Wolff (). Exploration of the Universe (ed. fifth). Saunders College Publishing. Parametru necunoscut
|last-author-amp=ignorat (ajutor) - Linton, Christopher (2004). From Eudoxus to Einstein. Cambridge: University Press. ISBN 0-521-82750-7
- Swetz, Frank; et al. (1997). Learn from the Masters!. Mathematical Association of America. ISBN 0-88385-703-0
- Andrea Milani and Giovanni F. Gronchi. Theory of Orbit Determination (Cambridge University Press; 378 pages; 2010). Discusses new algorithms for determining the orbits of both natural and artificial celestial bodies.
Legături externe
modificare- CalcTool: Orbital period of a planet calculator. Has wide choice of units. Requires JavaScript.
- Java simulation on orbital motion. Requires Java.
- NOAA page on Climate Forcing Data includes (calculated) data on Earth orbit variations over the last 50 million years and for the coming 20 million years
- On-line orbit plotter. Requires JavaScript.
- Orbital Mechanics (Rocket and Space Technology)
- Orbital simulations by Varadi, Ghil and Runnegar (2003) provide another, slightly different series for Earth orbit eccentricity, and also a series for orbital inclination. Orbits for the other planets were also calculated, by F. Varadi; B. Runnegar; M. Ghil (). „Successive Refinements in Long-Term Integrations of Planetary Orbits”. The Astrophysical Journal. 592: 620–630. Bibcode:2003ApJ...592..620V. doi:10.1086/375560., but only the eccentricity data for Earth and Mercury are available online.
- Understand orbits using direct manipulation. Requires JavaScript and Macromedia
- Merrifield, Michael. „Orbits (including the first manned orbit)”. Sixty Symbols. Brady Haran for the University of Nottingham.
- Planetary orbit Simulator Astronoo
[[Categorie:Orbite]]