Hebesfenomegacoroană

Descriere
Hebesfenomegacoroană

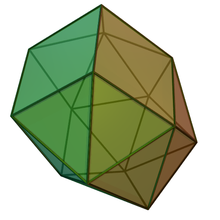(model 3D)
Tip	poliedru Johnson J₈₈ – J₈₉ – J₉₀
Fețe	21 (18 triunghiuri echilaterale, 3 pătrate)^[1]
Laturi (muchii)	33^[1]
Vârfuri	14^[1]
χ	2
Configurația vârfului	4 (3².4²); 6 (3⁵); 4 (3⁴.4)
Grup de simetrie	C_2v , [2], [*22], ordin 4
Arie	≈ 10,794 a² (a = latura)
Volum	≈ 2,913 a³ (a = latura)
Poliedru dual	–
Proprietăți	Convex
Desfășurată

În geometrie hebesfenomegacoroana este unul dintre poliedrele Johnson, (J₈₉).^[1]^[2] Este unul dintre poliedrele elementare Johnson care nu se pot obține prin „tăiere și lipire” ale poliedrelor platonice sau arhimedice. Având 21 de fețe, este un enicosaedru.

Construcție modificare

Johnson folosește prefixul hebesfeno- pentru a se referi la un complex asemănător unei pene format din trei lunule adiacente (o lunulă fiind un pătrat cu triunghiuri echilaterale atașate pe laturile opuse). De asemenea, sufixul -megacoroană se referă la un complex în formă de coroană format din 12 triunghiuri, în contrast cu complexul mai mic, format din 8 triunghiuri, din sfenocoroană. Unirea ambelor complexe produce hebesfenomegacoroana.^[2]

Mărimi asociate modificare

Coordonate carteziene modificare

Pentru a calcula coordonatele carteziene pentru hebesfenomegacoronă, fie $a$ ≈ 0,21684 a doua cea mai mică rădăcină pozitivă a polinomului de gradul 10

{\begin{aligned}&26880x^{10}+35328x^{9}-25600x^{8}-39680x^{7}+6112x^{6}\\&+13696x^{5}+2128x^{4}-1808x^{3}-1119x^{2}+494x-47\end{aligned}}

Atunci, coordonatele carteziene ale unei hebesfenomegacoroane cu lungimea laturilor 2 sunt date de reuniunea orbitelor punctelor

{\begin{aligned}&\left(1,1,2{\sqrt {1-a^{2}}}\right),\ \left(1+2a,1,0\right),\ \left(0,1+{\sqrt {2}}{\sqrt {\frac {2a-1}{a-1}}},-{\frac {2a^{2}+a-1}{\sqrt {1-a^{2}}}}\right),\ \left(1,0,-{\sqrt {3-4a^{2}}}\right),\\&\left(0,{\frac {{\sqrt {2(3-4a^{2})(1-2a)}}+{\sqrt {1+a}}}{2(1-a){\sqrt {1+a}}}},{\frac {(2a-1){\sqrt {3-4a^{2}}}}{2(1-a)}}-{\frac {\sqrt {2(1-2a)}}{2(1-a){\sqrt {1+a}}}}\right)\end{aligned}}

sub acțiunea grupului generat de reflexiile față de planele $xz$ și $yz$ .^[3]

Arie și volum modificare

Următoarele formule pentru arie, $A$ ^[1] și volum, $V$ sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:

A={\frac {3}{2}}(2+3{\sqrt {3}})\,a^{2}\approx 10,794229~a^{2},

Pentru volum se calculează $\xi$ ca rădăcina minimă pozitivă a polinomului de gradul 20:

47330370277129322496

x

²⁰

− 722445512980071186432

x

¹⁸

+ 3596480447590271287296

x

¹⁶

− 3596480447590271287296

x

¹⁴

+ 8973584611317745975296

x

¹²

− 3065290664181478981632

x

¹⁰

+ 366229890219212144640

x

⁸

− 8337259437908852736

x

⁶

− 22211277300912896

x

⁴

+ 132615435213216

x

²

+ 2693461945329 ,

cu care volumul este:

V=\xi \,a^{3}\approx 2,912910~a^{3}.

Note modificare

^ ^a ^b ^c ^d ^e en Stephen Wolfram, "Hebesphenomegacorona" from Wolfram Alpha. Retrieved March 4, 2023.
^ ^a ^b en Johnson, Norman W. (1966), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603
^ en Timofeenko, A. V. (2009). „The non-Platonic and non-Archimedean noncomposite polyhedra”. Journal of Mathematical Science. 162 (5): 718. doi:10.1007/s10958-009-9655-0. ISSN 1072-3374.

Legături externe modificare

Portal Matematică

en Eric W. Weisstein, Sphenomegacorona la MathWorld.
en Eric W. Weisstein, Johnson solid la MathWorld.

[SW-1] ^ ^a ^b ^c ^d ^e en Stephen Wolfram, "Hebesphenomegacorona" from Wolfram Alpha. Retrieved March 4, 2023.

[:0-2] Johnson, Norman W. (1966), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603

[3] Timofeenko, A. V. (2009). „The non-Platonic and non-Archimedean noncomposite polyhedra”. Journal of Mathematical Science. 162 (5): 718. doi:10.1007/s10958-009-9655-0. ISSN 1072-3374.

[1]

[2]

[3]