Bisfenocingulum

Descriere
Bisfenocingulum

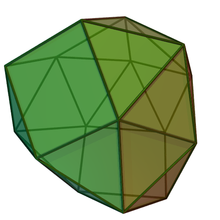(model 3D)
Tip	poliedru Johnson J₈₉ – J₉₀ – J₉₁
Fețe	24 (20 triunghiuri echilaterale, 4 pătrate)^[1]
Laturi (muchii)	38^[1]
Vârfuri	16^[1]
χ	2
Configurația vârfului	4 (3².4²); 4 (3⁵); 8 (3⁴.4)
Grup de simetrie	D_2d, [2⁺,4], (2*2), ordin 8
Arie	≈ 12,660 a² (a = latura)
Volum	≈ 3,778 a³ (a = latura)
Poliedru dual	Bisfenoid snub trunchiat de ordinul 5
Proprietăți	convexă
Desfășurată

În geometrie bisfenocingulum sau girobifastigium pentakis alungit este unul dintre poliedrele Johnson (J₉₀).^[1]^[2] Este unul dintre aceste poliedre care nu pot fi create prin operații de „divizare și lipire” ale poliedrelor platonice sau arhimedice. Având 24 de fețe, este un icositetraedru.

Dacă într-un bisfenocingulum se înlocuiește banda de triunghiuri de sus și de jos cu o bandă de dreptunghiuri, în timp ce se păstrează două sfenocoroane (J₈₆) opuse se obține ortobicupola pătrată, alt poliedru Johnson (J₂₈).

Mărimi asociate

Coordonate carteziene

Fie $a$ ≈0,76713 cea de a doua cea mai mică rădăcină pozitivă a polinomului

{\begin{aligned}&256x^{12}-512x^{11}-1664x^{10}+3712x^{9}\\&\quad +1552x^{8}-6592x^{7}+1248x^{6}+4352x^{5}\\&\quad -2024x^{4}-944x^{3}+672x^{2}-24x-23\end{aligned}}

și $h={\sqrt {2+8a-8a^{2}}},$ $c={\sqrt {1-a^{2}}}.$

Atunci coordonatele carteziene ale bisfenocingulumului cu latura de lungime 2 sunt date de reuniunea orbitelor punctelor

\left(1,2a,{\frac {h}{2}}\right),\ \left(1,0,2c+{\frac {h}{2}}\right),\ \left(1+{\frac {\sqrt {3-4a^{2}}}{c}},0,2c-{\frac {1}{c}}+{\frac {h}{2}}\right)

sub acțiunea grupului de simetrie generat de reflexiile față de planele $xz$ și $yz$ .^[3]

Arie și volum

Următoarele formule pentru arie, $A$ ^[1]^[4] și volum, $V$ sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) $a$ :

A=(4+5{\sqrt {3}})\,a^{2}\approx 12,660254\,a^{2}.

Pentru volum se calculează $\xi$ ca rădăcina minimă pozitivă a polinomului de gradul 24:

1213025622610333925376

x

²⁴

+ 54451372392730545094656

x

²²

− 796837093078664749252608

x

²⁰

− 4133410366404688544268288

x

¹⁸

+ 20902529024429842816303104

x

¹⁶

− 133907540390420673677230080

x

¹⁴

+ 246234688242991598853881856

x

¹²

− 63327534106871321714442240

x

¹⁰

+ 14389309497459555704164608

x

⁸

+ 48042947402464500749392128

x

⁶

− 5891096640600351061013664

x

⁴

− 3212114716816853362953264

x

²

+ 479556973248657693884401 ,

cu care volumul este:

V=\xi \,a^{3}\approx 3,777645~a^{3}.

Note

^ ^a ^b ^c ^d ^e en Stephen Wolfram, "Disphenocingulum" from Wolfram Alpha. Retrieved March 4, 2023.
^ en Johnson, Norman W. (1966), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603
^ en Timofeenko, A. V. (17 octombrie 2009). „The non-platonic and non-Archimedean noncomposite polyhedra”. Journal of Mathematical Sciences. 162 (5): 710–729. doi:10.1007/s10958-009-9655-0. ISSN 1072-3374.
^ en Disphenocingulum Calculator", rechneronline.de, accesat 2022-11-15

Legături externe

Portal Matematică

en Eric W. Weisstein, Disphenocingulum la MathWorld.
en Eric W. Weisstein, Johnson solid la MathWorld.

[SW-1] ^ ^a ^b ^c ^d ^e en Stephen Wolfram, "Disphenocingulum" from Wolfram Alpha. Retrieved March 4, 2023.

[2] Johnson, Norman W. (1966), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603

[3] Timofeenko, A. V. (17 octombrie 2009). „The non-platonic and non-Archimedean noncomposite polyhedra”. Journal of Mathematical Sciences. 162 (5): 710–729. doi:10.1007/s10958-009-9655-0. ISSN 1072-3374.

[rechner-4] Disphenocingulum Calculator", rechneronline.de, accesat 2022-11-15

[1]

[2]

[3]

[4]