Sfenocoroană augmentată
| Sfenocoroană augmentată | |
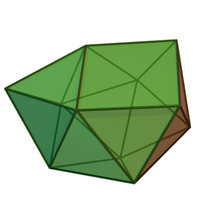 | |
| (model 3D) | |
| Descriere | |
|---|---|
| Tip | poliedru Johnson J86 – J87 – J88 |
| Fețe | 17 (16 triunghiuri echilaterale, 1 pătrat)[1] |
| Laturi (muchii) | 26[1] |
| Vârfuri | 11[1] |
| χ | 2 |
| Configurația vârfului | 1 (34); 2 (33.4) ; 6 (32.5); 2 (34.4) |
| Grup de simetrie | Cs , [ ], [*11], ordin 2 |
| Arie | ≈ 7,928 a2 (a = latura) |
| Volum | ≈ 1,751 a3 (a = latura) |
| Proprietăți | Convex |
| Desfășurată | |
 | |
În geometrie sfenocoroana augmentată este unul dintre poliedrele Johnson, (J87).[1][2] Este unul dintre poliedrele elementare Johnson care nu se pot obține prin „tăiere și lipire” ale poliedrelor platonice sau arhimedice. Având 17 fețe, este un heptadecaedru.
Construcție
modificareEste construit prin adăugarea unei piramide pătrate, (J1), pe una din fețele pătrate ale unei sfenocoroane, (J86). Este singurul poliedru Johnson care este obținut prin operații de „tăiere și lipire” în care componentele nu sunt toate prisme, antiprisme sau părți de poliedre platonice sau arhimedice.
Johnson folosește prefixul sfeno- pentru a se referi la un complex asemănător unei pene format din două lunule adiacente (o lunulă fiind un pătrat cu triunghiuri echilaterale atașate pe laturile opuse). De asemenea, sufixul -coroană se referă la un complex în formă de coroană, format din 8 triunghiuri echilaterale. Unirea ambelor complexe produce sfenocoroana.[2]
Mărimi asociate
modificareCoordonate carteziene
modificarePentru a calcula coordonatele carteziene pentru sfenocorona augmentată, se poate începe prin a calcula coordonatele sfenocoronei. Fie k ≈ 0,85273 cea mai mică rădăcină pozitivă a polinomului de gradul 4
Atunci, coordonatele carteziene ale unei sfenocorone cu lungimea laturilor 2 sunt date de reuniunea orbitelor punctelor
sub acțiunea grupului generat de reflexiile față de planele xz și yz.[3] Calcularea centroidului(d) și a versorului normal al uneia dintre fețele pătrate dă poziția ultimului vârf ca fiind
Arie și volum
modificareUrmătoarele formule pentru arie, A și volum, V sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:[1]
Note
modificare- ^ a b c d e en Stephen Wolfram, "Augmented sphenocorona" from Wolfram Alpha. Retrieved March 3, 2023.
- ^ a b en Johnson, Norman W. (), „Convex polyhedra with regular faces”, Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603
- ^ en Timofeenko, A. V. (). „The non-Platonic and non-Archimedean noncomposite polyhedra”. Journal of Mathematical Science. 162 (5): 718. doi:10.1007/s10958-009-9655-0.