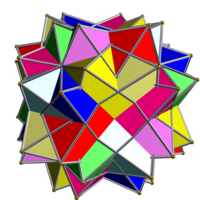
Compus de opt octaedre cu libertate de rotație
| Compus de opt octaedre cu libertate de rotație | |
 | |
| Descriere | |
|---|---|
| Tip | compus uniform UC10 - UC11 - UC12 |
| Fețe | 64 (triunghiuri) |
| Laturi (muchii) | 96 |
| Vârfuri | 48 |
| Configurația vârfului | 3.3.3.3[1] |
| Configurația feței | V4.4.4 |
| Grup de simetrie |
|
| Volum | ≈3,771 a3 (a = latura) |
| Proprietăți | Constituenți: 8 octaedre |
| Figura vârfului | |
 | |
În geometrie compusul de opt octaedre cu libertate de rotație este un compus poliedric uniform realizat dintr-un aranjament simetric de 8 octaedre, considerate ca antiprisme triunghiulare.[2]
Are indicele de compus uniform UC11.[2]
Construcție
modificarePoate fi construit prin suprapunerea a opt octaedre identice și apoi rotirea lor în perechi în jurul celor patru axe care trec prin centrele a două fețe opuse ale octaedrului. Fiecare octaedru este rotit cu un unghi egal (și opus, într-o pereche) θ.
Poate fi construit prin suprapunerea a doi compuși de patru octaedre cu libertate de rotație, unul rotit cu unghiul θ, iar celălalt rotit cu unghiul −θ.
Când θ = 0, toate cele opt octaedre coincid. Când θ este de 60°, octaedrele coincid în perechi dând două copii suprapuse ale compusului de patru octaedre.
Mărimi asociate
modificareCoordonate carteziene
modificareCoordonatele carteziene ale vârfurilor acestui compus sunt toate permutările lui
Volum
modificareUrmătoarea formulă pentru volum V este stabilită pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:
Imagini
modificare- Compus de opt octaedre cu libertate de rotație
-
Compusul cu θ = 0°
-
Compusul cu θ = 5°
-
Compusul cu θ = 10°
-
Compusul cu θ = 15°
-
Compusul cu θ = 20°
-
Compusul cu θ = 25°
-
Compusul cu θ = 30°
-
Compusul cu θ = 35°
-
Compusul cu θ = 40°
-
Compusul cu θ = 45°
-
Compusul cu θ = 50°
-
Compusul cu θ = 55°
-
Compusul cu θ = 60°
Note
modificareVezi și
modificare- Compuși de octaedre