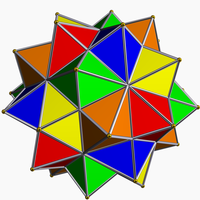
Compus de cinci octaedre

Compus de cinci octaedre
Descriere
Tip	compus poliedric regulat UC16 - UC17 - UC18
Fețe	40
Laturi (muchii)	60
Vârfuri	30
Configurația vârfului	3.3.3.3
Configurația feței	V4.4.4
Diagramă Coxeter	[5{3,4}]2{3,5}
Grup de simetrie	Compus: icosaedrică (Ih) Constituenți: piritoedrică (Th)
Poliedru dual	compus de cinci cuburi
Proprietăți	Constituenți: 5 octaedre
Figura vârfului

În geometrie compusul de cinci octaedre este unul dintre cei cinci compuși poliedrici regulați. Acest poliedru poate fi considerat fie o fațetare a unui icosidodecaedru, fie o stelare. Acest compus a fost descris pentru prima dată de Edmund Hess în 1876. Este unic printre compușii regulați prin faptul că nu are o anvelopă convexă regulată.

Compusul este o fațetare a icosidodecaedrului

Are indicele de compus uniform UC₁₇ și indicele Wenninger 23.

Compusul

Este un compus poliedric format din cinci octaedre dispuse în simetrie icosaedrică (I_h).

Poate fi construit și dintr-un triacontaedru rombic cu piramide cu baze rombice adăugate pe toate fețele, așa cum se arată în imaginea modelului cu cinci culori. (Această construcție nu generează compusul regulat de cinci octaedre, dar are aceeași topologie și poate fi deformat continuu în compusul regulat.)

Are o densitate mai nare decât 1.

Proiecțiile sferice și stereografice ale acestui compus arată la fel cu cele ale triacontaedrului disdiakis.
Vârfurile poliedrului convex pe axele de simetrie cu 3 și 5 poziții (gri în imaginile de mai jos) corespund doar traversărilor laturilor (muchiilor) compusului.

Poliedru sferic	Proiecții stereografice
	cu 2 poziții	cu 3 poziții	cu 5 poziții
Zonele din cercurile negre de mai jos corespund emisferei frontale a poliedrului sferic.

Ca stelare

Este a doua stelare a icosaedrului.

Diagrama stelării	Nucleul stelării	Anvelopa convexă
	Icosaedru	Icosidodecaedru

Dualul, compusul de cinci cuburi

Dual

Dualul său este compusul de cinci cuburi

Alt compus de cinci octaedre

Există încă un compus de cinci octaedre, cu simetrie octaedrică. Poate fi generat prin adăugarea unui al cincilea octaedru la compusul de patru octaedre.

Bibliografie

• de E. Hess, Zugleich Gleicheckigen und Gleichflächigen Polyeder, Schriften der Gesellschaft zur Berörderung der Gasammten Naturwissenschaften zu Marburg 11, 1876, pp. 5–97.
• en Coxeter, H.S.M.; Du Val, P.; Flather, H. T.; Petrie, J. F. (1999). The Fifty-Nine Icosahedra (ed. 3rd). Tarquin. ISBN 978-1-899618-32-3. MR 0676126.  (1st Edn University of Toronto (1938))
• en H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN: 0-486-61480-8, 3.6 The five regular compounds, pp.47-50, 6.2 Stellating the Platonic solids, pp.96-104
• en Cromwell, Peter R. (1997), Polyhedra, Cambridge . p 360
• en Harman, Michael G. (1974), Polyhedral Compounds, unpublished manuscript .
• en Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. 
• en Skilling, John (1976), „Uniform Compounds of Uniform Polyhedra”, Mathematical Proceedings of the Cambridge Philosophical Society, 79: 447–457, doi:10.1017/S0305004100052440, MR 0397554 .
• en Cundy, H. and Rollett, A. "Five Cubes in a Dodecahedron." §3.10.6 in Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 135–136, 1989.

Vezi și

• Lista compușilor poliedrici uniformi

Compuși regulați

• Compus de două tetraedre
• Compus de cinci tetraedre
• Compus de zece tetraedre
• Compus de cinci cuburi

Compuși de octaedre

• Compus de trei octaedre
• Compus de patru octaedre
• Compus de patru octaedre cu libertate de rotație
• Compus de șase octaedre
• Compus de opt octaedre cu libertate de rotație
• Compus de zece octaedre
• Compus de douăzeci de octaedre

Legături externe

• Materiale media legate de compus de cinci octaedre la Wikimedia Commons
• en MathWorld: Octahedron5-Compound
• en Paper Model Compound of Five Octahedra
• en Modelul VRML^{[nefuncțională]}
• Klitzing, Richard. „3D compound”. 
• en Polyhedron Category C1: Compounds Regulars Se

Selecție din cele 59 de posibile stelări ale icosaedrului
Regulat	Duale ale uniformelor		Compuși regulați			Stelare regulată	Altele
Icosaedru (convex)	Micul icosaedru triambic	Marele icosaedru triambic	Compus de cinci octaedre	Compus de cinci tetraedre	Compus de zece tetraedre	Marele icosaedru	Dodecaedru excavat	Stelarea finală
Procesul de stelare al icosaedrului creează un număr de poliedre și compuși înrudiți, cu simetrie icosaedrică.