Cupolă alungită
poliedru construit prin lipirea unei cupole cu o prismă
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici. |
| Cupolă alungită | |
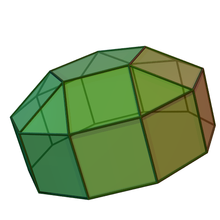 | |
| Exemplu: cupolă pentagonală alungită | |
| Descriere | |
|---|---|
| Fețe | n-triunghiuri, 3n pătrate, 1 n-gon, 1 2n-gon |
| Laturi (muchii) | 9n |
| Vârfuri | 5n |
| χ | 2 |
| Grup de simetrie | Cnv, [n], (*nn) |
| Grup de rotație | Cn, [n]+, (nn) |
| Proprietăți | convexă |
În geometrie, cupolele alungite sunt o mulțime infinită de poliedre, construite prin unirea unei cupole n-gonale cu o prismă 2n-gonală. Bazele la care are loc lipirea sunt cele congruente.
Există trei cupole alungite care sunt poliedre Johnson, făcute din triunghiuri echilaterale, pătrate și pentagoane regulate. Alăturarea unei prisme triunghiulare la un cub generează, de asemenea, un poliedru, dar are fețe adiacente coplanare, deci nu este un poliedru Johnson. Formele superioare pot fi construite doar fără toate fețele regulate, de exemplu cu triunghiuri isoscele.
Forme
modificare| n | Imagine | nume | fețe |
|---|---|---|---|
| 2 | fastigium alungit | 2 triunghiuri, 6+1 pătrate | |
| 3 | cupolă triunghiulară alungită (J18) | 3+1 triunghiuri, 9 pătrate, 1 hexagon | |
| 4 | cupolă pătrată alungită (J19) | 4 triunghiuri, 12+1 pătrate, 1 octogon | |
| 5 | cupolă pentagonală alungită (J20) | 5 triunghiuri, 15 pătrate, 1 pentagon, 1 decagon | |
| 6 | cupolă hexagonală alungită | 6 triunghiuri, 18 pătrate, 1 hexagon, 1 dodecagon |
Bibliografie
modificare- en Norman Johnson, "Convex Solids with Regular Faces", Canadian Journal of Mathematics, 18, 1966, pages 169–200. Conține enumerarea inițială a celor 92 de poliedre și conjectura că nu există altele.
- en Victor A. Zalgaller (). Convex Polyhedra with Regular Faces. Consultants Bureau. No ISBN. Prima demonstrație că există doar 92 de poliedre Johnson.
Vezi și
modificare