Prismă triunghiulară

Acest articol se referă la un corp geometric. Pentru o prismă de difracție, vedeți prismă (optică).

Descriere
Prismă triunghiulară uniformă

(model 3D)
Tip	poliedru prismatic uniform
Fețe	5 (2 triunghiuri, 3 paralelograme)
Laturi (muchii)	9
Vârfuri	6
χ	2
Configurația vârfului	4.4.3
Simbol Wythoff	2 3 \| 2
Simbol Schläfli	t{2,3} sau {3}×{}
Diagramă Coxeter
Grup de simetrie	D_3h, [3,2], (*322), ordin 12
Grup de rotație	D₃, [3,2]⁺, (322), ordin 6
Volum	$V={\frac {bhl}{2}}$
Poliedru dual	bipiramidă triunghiulară
Proprietăți	convexă
Figura vârfului

Desfășurată

În geometrie o prismă triunghiulară este o prismă cu trei fețe laterale; este un poliedru format dintr-o bază triunghiulară, o copie translată a ei și 3 fețe care unesc laturile bazelor. Ca poliedru cu cinci fețe, este un pentaedru.

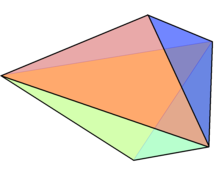
O prismă triunghiulară dreaptă are fețele laterale dreptunghiulare, altfel este oblică. O prismă triunghiulară uniformă este o prismă triunghiulară dreptunghiulară cu bazele triunghiuri echilaterale și fețele laterale pătrate.

Echivalent, este un poliedru în care două fețe sunt paralele, în timp ce normalele celor trei fețe laterale sunt în același plan (care nu este neapărat paralel cu planele bazelor). Aceste trei fețe sunt paralelograme. Toate secțiunile paralele cu bazele sunt congruente cu bazele.

Ca poliedru semiregulat (sau uniform)

O prismă triunghiulară dreaptă este un poliedru semiregulat sau, dacă fețele de bază sunt triunghiuri echilaterale, iar celelalte trei fețe sunt pătrate, un poliedru uniform. Ca poliedru uniform are simbolul U_76a. Acesta poate fi văzut ca un hosoedru trigonal trunchiat, reprezentat de simbolul Schläfli t{2,3}. Alternativ, poate fi văzut ca produsul cartezian al unui triunghi și al unui segment. Dualul său este bipiramida triunghiulară.

Grupul de simetrie al unei prisme drepte triunghiulare este D_3h de ordinul 12. Grupul de rotație^⁠(d) este D₃ de ordinul 6. Grupul de simetrie nu conține inversiunea față de centru.

Volum

Volumul oricărei prisme este produsul dintre aria bazei și distanța dintre cele două baze. În acest caz, baza este un triunghi, așa că trebuie pur și simplu să se calculeze aria triunghiului și să se înmulțească aceasta cu lungimea prismei:

V={\frac {bhl}{2}},

unde $b$ este lungimea unei laturi a triunghiului, $h$ este lungimea înălțimii ridicate pe acea latură, iar $l$ este distanța dintre baze.

Prismă triunghiulară trunchiată

O prismă triunghiulară dreaptă trunchiată are o față triunghiulară trunchiată oblic la un unghi față de baza inițială.^[1]

Volumul unei prisme triunghiulare trunchiate cu aria bazei A și cele trei înălțimi h₁, h₂ și h₃ este determinat de^[2]

V={\frac {A(h_{1}+h_{2}+h_{3})}{3}}.

Fațetare

Există două fațetări cu simetrie D_3h complete ale unei prisme triunghiulare, ambele cu 6 fețe în formă de triunghi isoscel, una conservând triunghiurile inițiale de sus și de jos și cealaltă conservând pătratele inițiale. Două fațetări cu simetrie C_3v inferioară au un triunghi ca bază, 3 fețe laterale pătrate intersectate și 3 fețe laterale triunghiulare isoscele.

Convexă	Fațetări
Simetrie D_3h			Simetrie C_3v

2 {3} 3 {4}	3 {4} 6 ( ) v { }	2 {3} 6 ( ) v { }	1 {3} 3 t'{2} 6 ( ) v { }	1 {3} 3 t'{2} 3 ( ) v { }

Poliedre și pavări înrudite

Un tetraedru regulat (bisfenoid tetragonal) poate fi divizat în două jumătăți de un pătrat central. Fiecare jumătate este topologic o prismă triunghiulară.

Familia prismelor n-gonale uniforme
Denumirea prismei	Prismă digonală	Prismă triunghiulară	Prismă tetragonală	Prismă pentagonală	Prismă hexagonală	Prismă heptagonală	Prismă octogonală	Prismă eneagonală	Prismă decagonală	Prismă endecagonală	Prismă dodecagonală	...	Prismă apeirogonală
Imagine												...
Pavare sferică												Pavare plană
Config. vârfului	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Diagramă Coxeter												...

Familia cupolelor convexe
n	2	3	4	5	6
Schläfli	{2} \|\| t{2}	{3} \|\| t{3}	{4} \|\| t{4}	{5} \|\| t{5}	{6} \|\| t{6}
Cupolă	Cupolă digonală	Cupolă triunghiulară	Cupolă pătrată	Cupolă pentagonală	Cupolă hexagonală (plată)
Poliedre uniforme înrudite	Prismă triunghiulară	Cubocta- edru	Rombi- cubocta- edru	Romb- icosidodeca- edru	Pavare rombi- trihexagonală

Variante de simetrie

Acest poliedru este înrudit topologic ca parte a secvenței de poliedre trunchiate uniforme cu configurațiile vârfurilor cu simetriile grupurilor Coxeter (3.2n.2n) și [n,3].

Variante ale pavărilor trunchiate cu simetrie *n32: t{n,3}
Smetrie *n32 [n,3]	Sferice				Euclid.	Hiperb. compacte		Paracomp.	Hiperbolice necompacte
Smetrie *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Figuri trunchiate
Schläfli	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{∞,3}	t{12i,3}	t{9i,3}	t{6i,3}
Figuri triakis
Config.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞

Acest poliedru este înrudit topologic ca parte a secvenței de poliedre cantelate cu figura vârfurilor (3.4.n.4) și continuă ca pavări ale planului hiperbolic. Aceste figuri tranzitive pe vârfuri au simetrie (*n32).

Variante de pavări expandate cu simetrie *n32: 3.4.n.4
Simetrie *n32 [n,3]	Sferice				Euclid.	Hiperb. compacte		Paracomp.
Simetrie *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Imagine
Vârf	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.∞.4

Compuși

Există 4 compuși uniformi ai prismelor triunghiulare:

compus de patru prisme triunghiulare, compus de opt prisme triunghiulare, compus de zece prisme triunghiulare, compus de douăzeci de prisme triunghiulare.

Faguri

Există 9 faguri uniformi care au celule în formă de prisme triunghiulare:

fagure cubic alternat giroalungit, fagure cubic alternat alungit, fagure prismatic triunghiular girat, fagure prismatic pătrat snub, fagure prismatic triunghiular, fagure prismatic triunghiular-hexagonal, fagure prismatic hexagonal trunchiat, fagure prismatic rombitriunghiular-hexagonal, fagure prismatic triunghiular-hexagonal snub, fagure prismatic triunghiular alungit.

Politopuri înrudite

Prisma triunghiulară este prima dintr-o serie dimensională de politopuri semiregulate. Fiecare politop uniform progresiv este construit pe baza figurii vârfului care este politopul anterior. Thorold Gosset a identificat această serie în 1900, politopurile conținând toate fațetele politopurilor regulate, toate simplexurile și ortoplexurile (triunghiuri echilaterale și pătrate în cazul prismei triunghiulare). În notația Coxeter prismei triunghiulare i se dă simbolul −1₂₁.

Politopuri k₂₁ în spațiul n-dimensional
Spațiu	Finit						Euclidian	Hiperbolic
E_n	3	4	5	6	7	8	9	10
Grup Coxeter	$E_{3}=A_{2}A_{1}$	$E_{4}=A_{4}$	$E_{5}=D_{5}$	$E_{6}$	$E_{7}$	$E_{8}$	$E_{9}={\tilde {E}}_{8}=E_{8}^{+}$	$E_{10}={\bar {T}}_{8}=E_{8}^{++}$
Diagramă Coxeter
Simetrie	[3^−1,2,1]	[3^0,2,1]	[3^1,2,1]	[3^2,2,1]	[3^3,2,1]	[3^4,2,1]	[3^5,2,1]	[3^6,2,1]
Ordin	12	120	1920	51 840	2 903 040	696 729 600	∞
Graf							–	–
Nume	−1₂₁	0₂₁	1₂₁	2₂₁	3₂₁	4₂₁	5₂₁	6₂₁

În spațiul cvadridimensional

Prisma triunghiulară există ca celule ale unui număr de 4-politopuri uniforme, inclusiv:

Politopuri cvadridimensionale cu prisme triunghiulare
Prismă tetraedrică	Prismă octaedrică	Prismă cuboctaedrică	Prismă icosaedrică	Prismă icosidodecaedrică	Prismă dodecaedrică trunchiată

Prismă rombicosi- dodecaedrică	Prismă rombi- cuboctaedrică	Prismă cubică trunchiată	Prismă dodecaedrică snub	Prismă antiprismatică n-gonală

5-celule cantelat	5-celule cantitrunchiat	5-celule runcinat	5-celule runcitrunchiat

Tesseract cantelat	Tesseract cantitrunchiat	Tesseract runcinat	Tesseract runcitrunchiat

24-celule cantelat	24-celule cantitrunchiat	24-celule runcinat	24-celule runcitrunchiat

120-celule cantelat	120-celule cantitrunchiat	120-celule runcinat	120-celule runcitrunchiat

Note

^ en Kern, William F.; Bland, James R. (1938). Solid Mensuration with proofs. p. 81. OCLC 1035479.
^ en „Volume of truncated prism”. Mathematics Stack Exchange. Accesat în 9 iulie 2019.

Bibliografie

en Eric W. Weisstein, Triangular prism la MathWorld.
en Interactive Polyhedron: Triangular Prism
en Surface area and volume of a triangular prism Arhivat în 25 mai 2022, la Wayback Machine.

Vezi și

Familia prismelor n-gonale uniforme
Denumirea prismei	Prismă digonală	Prismă triunghiulară	Prismă tetragonală	Prismă pentagonală	Prismă hexagonală	Prismă heptagonală	Prismă octogonală	Prismă eneagonală	Prismă decagonală	Prismă endecagonală	Prismă dodecagonală	...	Prismă apeirogonală
Imagine												...
Pavare sferică												Pavare plană
Config. vârfului	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
Diagramă Coxeter												...

Legături externe

Portal Matematică

Materiale media legate de prismă triunghiulară la Wikimedia Commons
en Klitzing, Richard. „3D uniform polyhedra”. Cheie: trip

[1] Kern, William F.; Bland, James R. (1938). Solid Mensuration with proofs. p. 81. OCLC 1035479.

[2] „Volume of truncated prism”. Mathematics Stack Exchange. Accesat în 9 iulie 2019.

[1]

[2]