Icosaedru triakis

Descriere
Icosaedru triakis

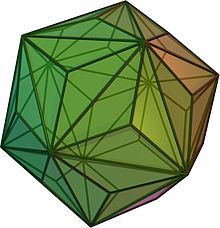(animație și model 3D)
Tip	Poliedru Catalan
Fețe	60 triunghiuri isoscele
Laturi (muchii)	90
Vârfuri	32
χ	2
Configurația vârfului	20{3}+12{10}
Simbol Conway	kI
Diagramă Coxeter
Grup de simetrie	I_h, H₃, [5,3], (*532)
Grup de rotație	I, [5,3]⁺, (532)
Unghi diedru	160° 36′ 45″ = arccos(−24 + 15√5/61)
Poliedru dual	Dodecaedru trunchiat
Proprietăți	Poliedru convex, tranzitiv pe fețe
Desfășurată

În geometrie un icosaedru triakis este un poliedru Catalan cu 60 de fețe. Fiecare poliedru Catalan este dualul unui poliedru arhimedic. Dualul icosaedrului triakis este dodecaedrul trunchiat. Este tranzitiv pe fețe.

Coordonate carteziene și dimensiuni

Fie $\varphi$ secțiunea de aur. Cele 12 puncte date de $(0,\pm 1,\pm \varphi )$ și permutările ciclice ale acestor coordonate sunt vârfurile unui icosaedru regulat. Dualul său, dodecaedrul regulat, ale cărui laturi intersectează pe cele ale icosaedrului în unghi drept, are ca vârfuri punctele $(\pm 1,\pm 1,\pm 1)$ împreună cu punctele $(\pm \varphi ,\pm 1/\varphi ,0)$ și permutările ciclice ale acestor coordonate.^[1] Înmulțind toate coordonatele acestui dodecaedru cu factorul $(7\varphi -1)/11\approx 0,938\,748\,901\,93$ se obține un dodecaedru ceva mai mic. Cele 20 de vârfuri ale acestui dodecaedru, împreună cu vârfurile icosaedrului, sunt vârfurile unui icosaedru triakis centrat în origine. Lungimea laturilor sale lungi este de $2$ . Fețele sale sunt triunghiuri isoscele cu un unghi obtuz de $\arccos(-3\varphi /10)\approx 119,009\,350\,869\,29^{\circ }$ și două ascuțite de $\arccos((\varphi +7)/10)\approx 30,480\,324\,565\,36^{\circ }$ . Raportul lungimilor laturilor lungi și scurte ale acestor triunghiuri este $(\varphi +7)/5\approx 1,723\,606\,797\,75$ .

Proiecții ortogonale

Icosaedrul triakis are trei proiecții ortogonale particulare: una pe mijlocul laturilor și două pe vârfuri: ultimele două corespund planelor Coxeter A₂ și H₂.

Proiecții ortogonale sub formă de cadre de sârmă
Simetrie proiectivă	[2]	[6]	[10]
Imagini
Imagini duale

Poliedre asemănătoare

Galeria prezintă o stelare și patru Kleetopuri ale icosaedrului triakis, cu piramide de diferite înălțimi.^[2]

Marele dodecicosacron, una dintre numeroasele stelări ale icosaedrul triakis.^[3]
Icosaedru augmentat cu piramide triunghiulare pe fiecare față; adică este un Kleetop al icosaedrului. Această interpretare este exprimată de numele „triakis”.^[4]
„Prima stelare a icosaedrului” sau micul icosaedru triambic,^[5] uneori numit, printre altele, „icosaedru triakis”
Marele dodecaedru stelat (cu piramide foarte înalte)
Marele dodecaedru (cu piramide inversate)

Poliedre înrudite

Icosaedrul triakis sferic

Este înrudit topologic ca parte a secvenței de poliedre trunchiate uniforme cu configurațiile vârfurilor (3.2n.2n) și simetriile grupului Coxeter [n,3].

Familia de poliedre icosaedrice uniforme
Simetrie: [5,3], (*532)							[5,3]⁺, (532)


{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duale ale poliedrelor uniforme

V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Icosaedrul triakis face parte dintr-o secvență de poliedre și pavări care se extinde în spațiul hiperbolic. Aceste figuri tranzitive pe fețe au simetria (*n32) în notația orbifold.

Variante ale pavărilor trunchiate cu simetrie *n32: t{n,3}
Smetrie *n32 [n,3]	Sferice				Euclid.	Hiperb. compacte		Paracomp.	Hiperbolice necompacte
Smetrie *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
Figuri trunchiate
Schläfli	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{∞,3}	t{12i,3}	t{9i,3}	t{6i,3}
Figuri triakis
Config.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞

Note

^ en Koca, Mehmet; Ozdes Koca, Nazife; Koc, Ramazon (2010). „Catalan Solids Derived From 3D-Root Systems and Quaternions”. Journal of Mathematical Physics. 51 (4). arXiv:0908.3272  . doi:10.1063/1.3356985.
^ en Brigaglia, Aldo; Palladino, Nicla; Vaccaro, Maria Alessandra (2018). „Historical notes on star geometry in mathematics, art and nature”. În Emmer, Michele; Abate, Marco. Imagine Math 6: Between Culture and Mathematics. Springer International Publishing. pp. 197–211. doi:10.1007/978-3-319-93949-0_17.
^ en Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. p. 270. ISBN 0-521-66405-5.
^ en Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). The Symmetries of Things. AK Peters. p. 284. ISBN 978-1-56881-220-5.
^ en Grünbaum, Branko (2008). „Can every face of a polyhedron have many sides?”. Geometry, games, graphs and education. The Joe Malkevitch Festschrift. Papers from Joe Fest 2008, York College–The City University of New York (CUNY), Jamaica, NY, USA, November 8, 2008. Bedford, MA: Comap, Inc. pp. 9–26. hdl:1773/4593. ISBN 978-1-933223-17-9. Zbl 1185.52009.

Bibliografie

en Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)
en Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
en Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 978-0-521-54325-5. MR 0730208. (The thirteen semiregular convex polyhedra and their duals, Page 19, Triakisicosahedron)

Legături externe

en Eric W. Weisstein, Triakis icosahedron la MathWorld.
en Eric W. Weisstein, Catalan solid la MathWorld.
en Triakis Icosahedron – Interactive Polyhedron Model

Portal Matematică

[1] Koca, Mehmet; Ozdes Koca, Nazife; Koc, Ramazon (2010). „Catalan Solids Derived From 3D-Root Systems and Quaternions”. Journal of Mathematical Physics. 51 (4). arXiv:0908.3272  . doi:10.1063/1.3356985.

[2] Brigaglia, Aldo; Palladino, Nicla; Vaccaro, Maria Alessandra (2018). „Historical notes on star geometry in mathematics, art and nature”. În Emmer, Michele; Abate, Marco. Imagine Math 6: Between Culture and Mathematics. Springer International Publishing. pp. 197–211. doi:10.1007/978-3-319-93949-0_17.

[3] Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. p. 270. ISBN 0-521-66405-5.

[4] Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). The Symmetries of Things. AK Peters. p. 284. ISBN 978-1-56881-220-5.

[5] Grünbaum, Branko (2008). „Can every face of a polyhedron have many sides?”. Geometry, games, graphs and education. The Joe Malkevitch Festschrift. Papers from Joe Fest 2008, York College–The City University of New York (CUNY), Jamaica, NY, USA, November 8, 2008. Bedford, MA: Comap, Inc. pp. 9–26. hdl:1773/4593. ISBN 978-1-933223-17-9. Zbl 1185.52009.

[1]

[2]

[3]

[4]

[5]