Cantelare
operație care teșește laturile și vârfurile unui politop regulat
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici. |
Pentru poliedre și pavări cantelarea corespunde deplasării fețelor formei regulate mai departe de centru, și completarea cu fețe noi a golurilor care apar în dreptul laturilor și vârfurilor inițiale. Operația mai este numită de către Alicia Boole Stott și expandare.
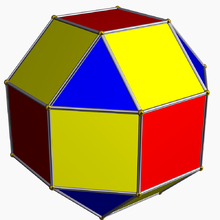
Notații
modificareUn politop cantelat este reprezentat de un simbol Schläfli extins t0,2{p,q,...} sau r sau rr{p,q,...}.
Pentru poliedre, cantelarea oferă o metodă directă de transformare a unui poliedru regulat în dualul său.
Exemplu: secvența de cantelare de la cub la octaedru.
| (poliedru regulat) cub |
cantelat 1/4 (cub teșit) |
cantelat uniform rombicuboctaedru |
cantelat 3/4 (octaedru teșit) |
(dual regulat) octaedru |
Alt exemplu: un cuboctaedru este un tetraedru cantelat.
Pentru politopurile din dimensiuni superioare, cantelarea oferă o metodă directă de transformare de la un politop regulat la forma sa birectificată.
Exemple de poliedre și pavări cantelate
modificare| Tip | Poliedre | Pavări | |||
|---|---|---|---|---|---|
| Coxeter | rTT | rCO | rID | rQQ | rHΔ |
| Notația Conway |
eT | eC = eO | eI = eD | eQ | eH = eΔ |
| Poliedre de cantelat |
Tetraedru | Cub sau octaedru |
Icosaedru or dodecaedru |
Pavare pătrată | Pavare hexagonală Pavare triunghiulară |
| Imagine | |||||
| Animație | |||||
| Coxeter | rrt{2,3} | rrs{2,6} | rrCO | rrID |
|---|---|---|---|---|
| Notația Conway |
eP3 | eA4 | eaO = eaC | eaI = eaD |
| Poliedre de cantelat |
Prismă triunghiulară sau Bipiramidă |
Antiprismă pătrată sau Trapezoedru tetragonal |
Cuboctaedru sau dodecaedru rombic |
Icosidodecaedru sau triacontaedru rombic |
| Imagine | ||||
| Animație |
Bibliografie
modificare- en Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN: 0-486-61480-8 (pp.145-154 Chapter 8: Truncation, p 210 Expansion)
- en Norman Johnson, Uniform Polytopes, Manuscript (1991)
- en Norman Johnson, The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
Legături externe
modificare- en Eric W. Weisstein, Expansion la MathWorld.
| Operatori poliedrici | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sămânță | Trunchiere | Rectificare | Bitrunchiere | Dual | Expandare | Omnitrunchiere | Alternări | ||
| t0{p,q} {p,q} |
t01{p,q} t{p,q} |
t1{p,q} r{p,q} |
t12{p,q} 2t{p,q} |
t2{p,q} 2r{p,q} |
t02{p,q} rr{p,q} |
t012{p,q} tr{p,q} |
ht0{p,q} h{q,p} |
ht12{p,q} s{q,p} |
ht012{p,q} sr{p,q} |