Poliedru cvasiregulat

Figuri cvasiregulate Domenii ale triunghiurilor dreptunghice (p q 2), = r{p,q} r{4,3} r{5,3} r{6,3} r{7,3}... r{∞,3} (3.4)2 (3.5)2 (3.6)2 (3.7)2 (3.∞)2 Domenii ale triunghiurilor isoscele (p p 3), = = h{6,p} h{6,4} h{6,5} h{6,6} h{6,7}... h{6,∞} = = = = = (4.3)4 (5.3)5 (6.3)6 (7.3)7 (∞.3)∞ Domenii ale triunghiurilor isoscele (p p 4), = = h{8,p} h{8,3} h{8,5} h{8,6} h{8,7}... h{8,∞} = = = = = (4.3)3 (4.5)5 (4.6)6 (4.7)7 (4.∞)∞ Domeniul triunghiului scalen (5 4 3), (3.5)4 (4.5)3 (3.4)5 Un poliedru sau pavare cvasiregulată are exact două tipuri de fețe regulate, care alternează în jurul fiecărui vârf. Figurile vârfurilor lor sunt poligoane izogonale.

Figuri regulate și cvasiregulte Domenii ale triunghiurilor dreptunghice (p p 2), = = r{p,p} = {p,4}1⁄2 {3,4}1⁄2 r{3,3} {4,4}1⁄2 r{4,4} {5,4}1⁄2 r{5,5} {6,4}1⁄2 r{6,6}... {∞,4}1⁄2 r{∞,∞} = = = = = (3.3)2 (4.4)2 (5.5)2 (6.6)2 (∞.∞)2 Domenii ale triunghiurilor isoscele (p p 3), = = {p,6}1⁄2 {3,6}1⁄2 {4,6}1⁄2 {5,6}1⁄2 {6,6}1⁄2... {∞,6}1⁄2 = = = = = (3.3)3 (4.4)3 (5.5)3 (6.6)3 (∞.∞)3 Domenii ale triunghiurilor isoscele (p p 4), = = {p,8}1⁄2 {3,8}1⁄2 {4,8}1⁄2 {5,8}1⁄2 {6,8}1⁄2... {∞,8}1⁄2 = = = = = (3.3)4 (4.4)4 (5.5)4 (6.6)4 (∞.∞)4 Un poliedru sau pavare regulate pot fi considerate cvasiregulate dacă au un număr par de fețe în jurul fiecărui vârf (și astfel poate avea fețele colorate alternativ).

În geometrie un poliedru cvasiregulat este un poliedru uniform care are exact două tipuri de fețe regulate, care alternează în jurul fiecărui vârf. Ele sunt tranzitive pe vârfuri și pe laturi, deci mai apropiate de poliedrele regulate decât cele semiregulate, care sunt tranzitive doar pe vârfuri.

Dualele lor sunt tranzitive pe fețe și laturi; au exact două tipuri de figuri ale vârfului, regulate, care alternează în jurul fiecărei fețe. Uneori acestea sunt considerate și ele cvasiregulate.

Există doar două poliedre convexe cvasiregulate: cuboctaedrul și icosidodecaedrul. Numele lor, date de Kepler, provin din recunoașterea faptului că fețele lor sunt toate fețele perechii duale cub și octaedru în primul caz, și a perechii duale icosaedru și dodecaedru în cazul al doilea.

Aceste forme reprezentând o pereche a unei figuri regulate și duala acesteia pot primi un simbol Schläfli vertical ${\begin{Bmatrix}p\\q\end{Bmatrix}}$ sau r{p,q}, care să descrie faptul că fețele lor sunt toate fețele (în ordine diferită) ale celor două forme regulate, {p,q} și duala sa {q,p}. Un poliedru cvasiregulat cu acest simbol va avea o configurație a vârfului p.q.p.q (sau (p.q)²).

Mai general, o figură cvasiregulată poate avea configurația vârfului (p.q)^r, reprezentând r (2 sau mai multe) secvențe de fețe în jurul vârfului.

Pavările planului pot fi și ele cvasiregulate, de exemplu pavarea trihexagonală, cu configurația vârfului (3.6)². Alte pavări cvasiregulate există în planul hiperbolic, cum ar fi pavarea triheptagonală, (3.7)². Sau, în general: (p.q)², cu 1/p + 1/q < 1/2.

Poliedrele și pavările regulate cu un număr par de fețe la fiecare vârf pot fi considerate și cvasiregulate prin diferențierea între fețele de același ordin, prin reprezentarea lor diferită sau colorarea lor alternativă (fără a defini orientarea suprafeței). O figură regulată cu simbolul Schläfli {p,q} poate fi considerată cvasiregulată, cu configurația vârfului (p.p)^q/2, pentru q par.

Exemple

Octaedrul regulat, cu simbolul Schläfli {3,4}, deoarece 4 este par poate fi considerat cvasiregulat, ca tetratetraedru (2 seturi de 4 triunghiuri ale tetraedrului), cu configurația vârfului (3.3)^4/2 = (3_a.3_b)², alternând două culori ale fețelor triunghiulare.

Pavarea pătrată, cu configurația vârfului 4⁴, deoarece 4 este par poate fi considerată cvasiregulată, cu configurația vârfului (4.4)^4/2 = (4_a.4_b)², colorată ca tabla de șah.

Pavarea triunghiulară, cu configurația vârfului 3⁶, deoarece 6 este par poate fi considerată cvasiregulată, cu configurația vârfului (3.3)^6/2 = (3_a.3_b)³, alternând două culori ale fețelor triunghiulare.

Construcția Wythoff

Poliedre regulate (p | 2 q) și cvasiregulate (2 | p q) create prin Construcția Wythoff cu punctul generator într-unul dintre cele trei colțuri ale domeniului fundamental. Aceasta definește o singură latură din domeniul fundamental.

Poliedre cvasiregulate generate din toate cele 3 colțuri ale domeniului fundamental al triunghiurilor Schwarz care nu au unghiuri drepte:
q | 2 p, p | 2 q, 2 | p q

Coxeter definește un poliedru cvasiregulat ca având un simbol Wythoff de forma p | q r, poliedru care este regulat dacă q=2 sau q=r.

Diagrama Coxeter–Dynkin este o altă reprezentare simbolică care arată relația cvasiregulată dintre două forme duale regulate:

Simbol Schläfli		Diagramă Coxeter	Simbol Wythoff
${\begin{Bmatrix}p,q\end{Bmatrix}}$	{p,q}		q | 2 p
${\begin{Bmatrix}q,p\end{Bmatrix}}$	{q,p}		p | 2 q
${\begin{Bmatrix}p\\q\end{Bmatrix}}$	r{p,q}	or	2 | p q

Poliedrele cvasiregulate convexe

Articol principal: Rectificare (geometrie).

Există două poliedre uniforme cvasiregulate convexe:

1. cuboctaedrul ${\begin{Bmatrix}3\\4\end{Bmatrix}}$, cu configurația vârfului (3.4)² și diagrama Coxeter–Dynkin  ;
2. icosidodecaedrul ${\begin{Bmatrix}3\\5\end{Bmatrix}}$, cu configurația vârfului (3.5)² și diagrama Coxeter–Dynkin  .

În plus, octaedrul, care este și el regulat, ${\begin{Bmatrix}3\\3\end{Bmatrix}}$, cu configurația vârfului (3.3)², poate fi considerat cvasiregulat dacă fețele sale se colorează alternativ cu două culori. În această formă uneori este cunoscut sub numele de tetratetraedru. Poliedrele regulate convexe rămase au un număr impar de fețe la fiecare vârf, așa că nu pot fi colorate într-un mod care să păstreze tranzitivitatea pe laturi. Are diagrama Coxeter–Dynkin  .

Fiecare dintre acestea formează nucleul comun al unei perechi de poliedre duale regulate. Numele a două dintre acestea dau indicații pentru perechea duală asociată: cub $\cap$ octaedru, respectiv icosaedru $\cap$ dodecaedru. Octaedrul este nucleul comun a perechii duale de tetraedre (compusul cunoscut drept stella octangula); când este oținut astfel, octaedrul este uneori numit tetratetraedru, ca tetraedru $\cap$ tetraedru.

Regulat	Dual regulat	Nucleu comun cvasiregulat	Figura vârfului
Tetraedru {3,3} 3 | 2 3	Tetraedru {3,3} 3 | 2 3	Tetratetraedru r{3,3} 2 | 3 3	3.3.3.3
Cub {4,3} 3 | 2 4	Octaedru {3,4} 4 | 2 3	Cuboctaedru r{3,4} 2 | 3 4	3.4.3.4
Dodecaedru {5,3} 3 | 2 5	Icosaedru {3,5} 5 | 2 3	Icosidodecaedru r{3,5} 2 | 3 5	3.5.3.5

Oricare dintre aceste poliedre cvasiregulate poate fi construit printr-o operație de rectificare a oricăruia dintre poliedrele de proveniență regulate, trunchiind complet vârfurile, până când fiecare latură inițială este redusă la punctul său de mijloc.

Pavări cvasiregulate

Această secvență continuă ca pavarea trihexagonală, cu figura vârfului (3.6)² — o pavare cvasiregulată bazată pe pavarea triunghiulară și pavarea hexagonală.

Regulată	Regulată duală	Combinație cvasiregulată	Figura vârfului
Pavare hexagonală {6,3} 6 | 2 3	Pavare triunghiulară {3,6} 3 | 2 6	Pavare trihexagonală r{6,3} 2 | 3 6	(3.6)2

Modelul tablei de șah este o colorare cvasiregulată a pavării pătrate, cu figura vârfului (4.4)²:

Regulată	Regulată duală	Combinație cvasiregulată	Figura vârfului
{4,4} 4 | 2 4	{4,4} 4 | 2 4	r{4,4} 2 | 4 4	(4.4)2

Pavarea triunghiulară poate fi și ea considerată și cvasiregulată, cu trei seturi de triunghiuri alternante la fiecare vârf, (3.3)³:

h{6,3} 3 | 3 3 =

În planul hiperbolic această secvență continuă, de exemplu cu pavarea triheptagonală, cu figura vârfului (3.7)² - o pavare cvasiregulată bazată pe pavarea triunghiulară de ordinul 7 și pavarea heptagonală.

Regulat	Dual regulat	Combinație cvasiregulată	Figura vârfului
Pavare heptagonală {7,3} 7 | 2 3	Pavare triunghiulară {3,7} 3 | 2 7	Pavare triheptagonală r{3,7} 2 | 3 7	(3.7)2

Exemple neconvexe

Coxeter, H.S.M. și colab. (1954) clasifică și anumite poliedre stelate, având aceleași caracteristici, ca fiind cvasiregulate. Două se bazează pe perechi duale de poliedre Kepler–Poinsot, în același mod ca și la exemplele convexe:

1. marele icosidodecaedru ${\begin{Bmatrix}3\\5/2\end{Bmatrix}}$;
2. dodecadodecaedrul ${\begin{Bmatrix}5\\5/2\end{Bmatrix}}$.

Regulat	Dual regulat	Nucleu cvasiregulat comun	Figura vârfului
Marele dodecaedru stelat {5/2,3} 3 | 2 5/2	Marele icosaedru {3,5/2} 5/2 | 2 3	Marele icosidodecaedru r{3,5/2} 2 | 3 5/2	3.5/2.3.5/2
Micul dodecaedru stelat {5/2,5} 5 | 2 5/2	Marele dodecaedru {5,5/2} 5/2 | 2 5	Dodecadodecaedrul r{5,5/2} 2 | 5 5/2	5.5/2.5.5/2

Alte nouă sunt hemipoliedre, care sunt forme fațetate ale poliedrelor cvasiregulare menționate mai sus, derivate din rectificarea poliedrelor regulate. Acestea cuprind fețele ecuatoriale care trec prin centrul poliedrelor:

Cvasiregulat (rectificat)	Tetratetraedru	Cuboctaedru	Icosidodecaedru	Marele icosidodecaedru	Dodecadodecaedru
Cvasiregulat (hemipoliedre)	Tetrahemihexaedru 3/2 3 | 2	Octahemioctaedru 3/2 3 | 3	Micul icosihemidodecaedru 3/2 3 | 5	Marele icosihemidodecaedru 3/2 3 | 5/3	Micul dodecahemicosaedru 5/3 5/2 | 3
Figura vârfului	3.4.3/2.4	3.6.3/2.6	3.10.3/2.10	3.10/3.3/2.10/3	5/2.6.5/3.6
Cvasiregulat (hemipoliedre)		Cubohemioctaedru 4/3 4 | 3	Micul dodecahemidodecaedru 5/4 5 | 5	Marele dodecahemidodecaedru 5/3 5/2 | 5/3	Marele dodecahemicosaedru 5/4 5 | 3
Figura vârfului		4.6.4/3.6	5.10.5/4.10	5/2.10/3.5/3.10/3	5.6.5/4.6

În final, există trei forme ditrigonale, toate fațetele dodecaedrului regulat, ale căror figuri ale vârfului conțin trei alternanțe ale celor două tipuri de fețe:

Imagine	Fațetat din Simbol Wythoff Diagramă Coxeter	Figura vârfului
	Dodecadodecaedru ditrigonal 3 | 5/3 5 or	(5.5/3)3
	Micul icosidodecaedru ditrigonal 3 | 5/2 3 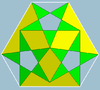or	(3.5/2)3
	Marele icosidodecaedru ditrigonal 3/2 | 3 5 or	((3.5)3)/2

În planul euclidian, secvența de hemipoliedre continuă cu următoarele patru pavări stelate, unde apeirogoanele apar ca poligoane ecuatoriale menționate mai sus:

Pavare inițială rectificată	Diagrama laturii	Corp	Config. vârf	Wythoff	Grup de simetrie
Pavare pătrată			4.∞.4/3.∞ 4.∞.-4.∞	4/3 4 | ∞	p4m
Pavare triunghiulară			(3.∞.3.∞.3.∞)/2	3/2 | 3 ∞	p6m
Pavare trihexagonală			6.∞.6/5.∞ 6.∞.-6.∞	6/5 6 | ∞
			∞.3.∞.3/2 ∞.3.∞.-3	3/2 3 | ∞

Duale cvasiregulate

Unele autorități susțin că, deoarece dualele poliedrelor cvasiregulate au aceleași simetrii, și aceste duale ar trebui să fie numite cvasiregulate. Dar nu toată lumea folosește această terminologie. Aceste duale sunt tranzitive pe laturile și fețele lor (dar nu și pe vârfurile lor); sunt poliedrele Catalan tranzitive pe laturi. Cele convexe sunt, în ordinea corespunzătoare ca mai sus:

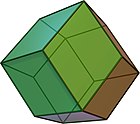
1. dodecaedrul rombic, cu două tipuri de vârfuri alternante, 8 cu trei fețe rombice și 6 cu patru fețe rombice;
2. triacontaedrul rombic, cu două tipuri de vârfuri alternante, 20 cu trei fețe rombice și 12 cu cinci fețe rombice.

În plus, prin dualitate cu octaedrul, cubul, care este de obicei regulat, poate fi făcut cvasiregulat dacă vârfurile alternate primesc culori diferite.

Configurațiile fețelor lor au forme V3.n.3.n și diagrama Coxeter–Dynkin

Cub V(3.3)2	Dodecaedru rombic V(3.4)2	Triacontaedru rombic V(3.5)2	Pavare rombică V(3.6)2	V(3.7)2	V(3.8)2

Aceste trei duale cvasiregulate sunt, de asemenea, caracterizate prin faptul că au fețele rombice. Acest model cu fețe rombice continuă ca V(3.6)², pavare rombică.

Politopuri și faguri cvasiregulați

În dimensiuni superioare, Coxeter a definit un politop sau un fagure cvasiregulat prin faptul de a avea fațete regulate și figuri ale vârfului cvasiregulate. Rezultă că toate figurile vârfurilor sunt congruente și că există două tipuri de fațete, care alternează.

În spațiul euclidian cvadridimensional 16-celule regulat poate fi văzut, de asemenea, ca fiind cvasiregulat ca un tesseract, h{4,3,3}, cu diagramele Coxeter: = , compus din celule alternative tetraedru și tetraedru. Figura vârfului este tetratetraedrul cvasiregulat (un octaedru cu simetrie tetraedrică), .

Singurul fagure cvasiregulat din spațiul euclidian tridimensional este fagurele cubic alternat, h{4,3,4}, cu diagramele Coxeter: = , compus din celule alternante tetraedrice și octaedrice. Figura sa de vârf este cuboctaedrul cvasiregulat, .

În spațiul hiperbolic tridimensional un fagure cvasiregulat este fagurele cubic alternat de ordinul 5, h{4,3,5}, cu diagramele Coxeter: = , compus din celule alternante tetraedrice și icosaedrice. Figura sa de vârf este icosidodecaedrul cvasiregulat, . Un fagure cubic alternat de ordinul 6 paracompact înrudit, h{4,3,6} are celule alternante tetraedrice și hexagonale de pavări cu figura vârfului o pavare trihexagonală cvasiregulată, .

Politopuri și faguri cvasiregulați: h{4,p,q}
Spațiu	Finit	Afin	Compact	Paracompact
Simbol Schläfli	h{4,3,3}	h{4,3,4}	h{4,3,5}	h{4,3,6}	h{4,4,3}	h{4,4,4}
	$\left\{3,{3 \atop 3}\right\}$	$\left\{3,{4 \atop 3}\right\}$	$\left\{3,{5 \atop 3}\right\}$	$\left\{3,{6 \atop 3}\right\}$	$\left\{4,{4 \atop 3}\right\}$	$\left\{4,{4 \atop 4}\right\}$
Diagramă Coxeter	↔	↔	↔	↔	↔	↔
	↔					↔
Imagine
Figura vârfului r{p,3}

Figura vârfului comună este tetratetraedrul cvasiregulat, , la fel ca octaedrul regulat

4-politopurile regulate sau fagurii de forma {p,3,4} sau pot avea simetria înjumătățită ca în formă cvasiregulată , creând celule {p,3} colorate alternativ. Aceste cazuri cuprind fagurele cubic euclidian {4,3,4} cu celule cubice, cel hiperbolic compact {5,3,4} cu celule dodecaedrice și cel paracompact {6,3,4} cu celule pavări hexagonale infinite. Au câte patru celule în jurul fiecărei laturi, alternând în 2 culori. Figurile vârfurilor lor sunt tetratetraedre cvasiregulate, = .

Faguri regulați și cvasiregulați: {p,3,4} și {p,31,1}
Spațiu	4-spațiu euclidian	3-spațiu euclidian	3-spțiu hiperbolic
Nume	{3,3,4} {3,31,1} = $\left\{3,{3 \atop 3}\right\}$	{4,3,4} {4,31,1} = $\left\{4,{3 \atop 3}\right\}$	{5,3,4} {5,31,1} = $\left\{5,{3 \atop 3}\right\}$	{6,3,4} {6,31,1} = $\left\{6,{3 \atop 3}\right\}$
Diagramă Coxeter	=	=	=	=
Imagine
Celule {p,3}

Figura vârfului comună este pavarea triunghiulară cvasiregulată, =

Similar, fagurii hiperbolici regulați de forma {p,3,6} sau pot avea simetria înjumătățită ca într-o formă cvasiregulată , formând celule {p,3} colorate alternat. Aceștia au câte șase celule în jurul fiecărei laturi, alternând în 2 culori. Figurile vârfurilor lor sunt pavări triunghiulare cvasiregulate, .

Faguri hiperbolici uniformi: {p,3,6} și {p,3^[3]}

Formă	Paracompact				Necompact
Nume	{3,3,6} {3,3[3]}	{4,3,6} {4,3[3]}	{5,3,6} {5,3[3]}	{6,3,6} {6,3[3]}	{7,3,6} {7,3[3]}	{8,3,6} {8,3[3]}	... {∞,3,6} {∞,3[3]}
Imagine
Celule	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}

Bibliografie

• en Cromwell, P. Polyhedra, Cambridge University Press (1977).
• en Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN: 0-486-61480-8, 2.3 Quasi-Regular Polyhedra. (p. 17), Quasi-regular honeycombs p.69

Legături externe

• en Eric W. Weisstein, Quasiregular polyhedron la MathWorld.
• en Eric W. Weisstein, Uniform polyhedron la MathWorld. Quasi-regular polyhedra: (p.q)^r
• en George Hart, Quasiregular polyhedra