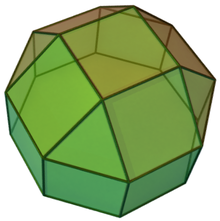
Cupolă pătrată alungită

Cupolă pătrată alungită
(model 3D)
Descriere
Tip	poliedru Johnson J18 – J19 – J20
Fețe	18 (4 triunghiuri echilaterale,     3×4+1 pătrate,     1 octogon regulat)
Laturi (muchii)	36
Vârfuri	20
χ	2
Configurația vârfului	8 (42.8); 4+8 (3.43)
Grup de simetrie	C4v, [4], (*44), ordin 8
Arie	≈ 19,560 a2   (a = latura)
Volum	≈   6,771 a3   (a = latura)
Poliedru dual	C1000dJ19
Proprietăți	convexă
Desfășurată

În geometrie cupola pătrată alungită este un poliedru convex construit prin alungirea unei cupole pătrate prin atașarea unei prisme octogonale la baza acesteia. Este poliedrul Johnson (J₁₉ ). Având 18 fețe, este un octadecaedru.

Poliedrul poate fi văzut ca un rombicuboctaedru cu unul dintre „capace” (o cupolă pătrată, J₄) îndepărtat.

Mărimi asociate

Următoarele formule pentru arie A, volum V și raza sferei care circumscrie poliedrul R sunt stabilite pentru lungimea laturilor tuturor poligoanelor (care sunt regulate) a:

$A=\left(15+2{\sqrt {2}}+{\sqrt {3}}\right)\,a^{2}\approx 19,560477\,a^{2},$

$V=\left(3+{\frac {8{\sqrt {2}}}{3}}\right)\,a^{3}\approx 6,771236\,a^{3},$

$R={\frac {1}{2}}{\sqrt {5+2{\sqrt {2}}}}\,a\approx 1,398966\,a\,.$

Poliedre și faguri înrudiți

Poliedru dual

Dualul cupolei pătrate alungite are 20 fețe: 8 triunghiuri isoscele, 4 romboedre și 8 patrulatere:

Dualul cupolei pătrate alungite	Desfășurata dualului

Faguri

Cupola pătrată alungită poate tesela spațiul împreună cu tetraedrul și cubul, sau împreună cu tetraedrul și cuboctaedrul, sau împreună ci tetraedrul, piramida pătrată alungită și bipiramida pătrată alungită.

Legături externe

• en Eric W. Weisstein, Elongated square cupola la MathWorld.
• en Eric W. Weisstein, Johnson solid la MathWorld.