Sfera Riemann

În matematică sfera Riemann, numită astfel după Bernhard Riemann, este un model matematic al planului complex extins: planul complex plus un punct de la infinit. Acest plan extins reprezintă numerele complexe extinse, adică numerele complexe plus valoarea $\infty$ pentru infinit. Cu modelul Riemann, punctul $\infty$ este aproape de numere foarte mari, la fel cum punctul $0$ este aproape de numerele foarte mici.

Sfera Riemann poate fi vizualizată ca un plan complex aplicat pe o sferă (printr-o formă de proiecție stereografică — detaliile sunt date în articol)

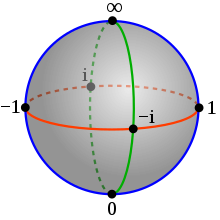
Numerele complexe extinse sunt utile în analiza complexă deoarece în anumite circumstanțe permit împărțirea cu zero, într-un mod bine definit, care dă expresii precum $1/0=\infty$. De exemplu, orice funcție rațională pe planul complex poate fi extinsă la o funcție olomorfă pe sfera Riemann, imaginile polilor funcției raționale fiind la infinit. În general, orice funcție meromorfă poate fi considerată ca o funcție olomorfă al cărei codomeniu este sfera Riemann.

În geometrie sfera Riemann este exemplul prototip al unei suprafețe Riemann^⁠(d) și este una dintre cele mai simple varietăți complexe. În geometria proiectivă, sfera poate fi considerată ca fiind dreapta proiectivă complexă $\mathbf {P} ^{1}(\mathbb {C} )$, spațiul proiectiv^⁠(d) al tuturor dreptelor complexe din $\mathbb {C} ^{2}$. Ca și în cazul oricărei suprafețe Riemann compacte, sfera poate fi văzută și ca o curbă algebrică^⁠(d) proiectivă, făcând-o un exemplu fundamental în geometria algebrică. De asemenea, își găsește utilitate în alte discipline care depind de analiză și geometrie, cum ar fi sfera Bloch^⁠(d) din mecanica cuantică și în alte ramuri ale fizicii.

Planul complex extins este numit și planul complex închis.

Numerele complexe extinse

Numerele complexe extinse constau din numerele complexe $\mathbb {C}$ împreună cu $\infty$. Mulțimea numerelor complexe extinse poate fi exprimată prin $\mathbb {C} \cup \{\infty \}$ și adesea este notată prin adăugarea unor diacritice la litera $\mathbb {C}$, cum ar fi

${\widehat {\mathbb {C} }},\quad {\overline {\mathbb {C} }},\quad$sau$\quad \mathbb {C} _{\infty }.$

Notația $\mathbb {C} ^{*}$ a fost folosită și ea, dar deoarece această notație este folosită și pentru planul perforat $\mathbb {C} \setminus \{0\}$, poate duce la ambiguități.

Din punct de vedere geometric, mulțimea numerelor complexe extinse este denumită sfera Riemann (sau planul complex extins).

Operații aritmetice

Adunarea numerelor complexe extinse poate fi extinsă prin definirea pentru $z\in \mathbb {C}$,

$z+\infty =\infty$

pentru orice număr complex $z$, iar înmulțirea poate fi extinsă prin

$z\times \infty =\infty$

pentru orice număr complex $z$ nenul, cu $\infty \times \infty =\infty$. De notat că operațiile $\infty -\infty$ și $0\times \infty$ sunt lăsate nedefinite. Spre deosebire de numerele complexe, numerele complexe extinse nu formează un corp deoarece $\infty$ nu are nici un element opus și nici un element invers. Totuși, se obișnuiește să se definească împărțirea pe $\mathbb {C} \cup \{\infty \}$ prin

${\frac {z}{0}}=\infty \quad$și$\quad {\frac {z}{\infty }}=0$

pentru toate numerele complexe $z$ nenule precum și $\infty /0=\infty$ și $0/\infty =0$. Câturile $0/0$ și $\infty /\infty$ rămân nedefinite.

Funcții raționale

Orice funcție rațională $f(z)=g(z)/h(z)$ (cu alte cuvinte, $f(z)$ este raportul funcțiilor polinomiale $g(z)$ și $h(z)$ din $z$ cu coeficienți complecși, astfel încât $g(z)$ și $h(z)$ nu are vreun factor comun) poate fi extinsă la o funcție continuă pe sfera Riemann. Mai exact, dacă $z_{0}$ este un număr complex astfel încât numitorul $h(z_{0})$ este zero, dar numărătorul $g(z_{0})$ este diferit de zero, atunci $f(z_{0})$ poate fi definit ca find $\infty$. Mai mult, $f(\infty )$ poate fi definită ca limita lui $f(z)$ la $z\to \infty$, limită care poate fi finită sau infinită.

Mulțimea funcțiilor raționale complexe — al căror simbol matematic este $\mathbb {C} (z)$ — formează toate funcțiile olomorfe posibile în sfera Riemann pe ea însăși, când este privită ca o suprafață Riemann^⁠(d), cu excepția funcției constante, care ia peste tot valoarea $\infty$. Funcțiile lui $\mathbb {C} (z)$ formează un corp algebric, cunoscut drept corpul funcțiilor raționale pe sferă.

De exemplu, fiind dată funcția

$f(z)={\frac {6z^{2}+1}{2z^{2}-50}}$

se poate defini $f(\pm 5)=\infty$, deoarece numitorul este zero la $\pm 5$ iar $f(\infty )=3$ deoarece $f(z)\to 3$ pentru $z\to \infty$. Folosind aceste definiții, $f$ devine o funcție continuă în sfera Riemann pe ea însăși.

Ca varietate complexă

Ca o varietate complexă unidimensională, sfera Riemann poate fi descrisă prin două reprezentări, ambele având domeniul egal cu planul numeric complex $\mathbb {C}$. Fie $\zeta$ un număr complex într-o copie a lui $\mathbb {C}$ și fie $\xi$ un număr complex într-o altă copie a lui $\mathbb {C}$. Se pune în corespondență fiecare număr complex $\zeta$ diferit de zero din primul $\mathbb {C}$ cu numărul complex $1/\xi$ diferit de zero din cel de-al doilea $\mathbb {C}$. Atunci aplicația

$f(z)={\frac {1}{z}}$

este numită aplicație de tranziție între cele două copii ale $\mathbb {C}$, asociindu-le. Deoarece aplicațiile de tranziție sunt funcții olomorfe, ele definesc o varietate complexă, numită sfera Riemann. Ca o varietate complexă de 1 dimensiune complexă (adică 2 dimensiuni reale), aceasta se mai numește și „suprafață Riemann”.

Intuitiv, aplicațiile de tranziție indică cum se „lipesc” împreună două plane pentru a forma sfera Riemann. Planele sunt „lipite” într-o manieră „interior-exterior”, astfel încât să se suprapună aproape peste tot^⁠(d), fiecare plan contribuind doar cu un punct (originea lui) lipsă din celălalt plan. Cu alte cuvinte, (aproape) orice punct din sfera Riemann are atât o valoare $\zeta$ cât și o valoare $\xi$, iar cele două valori sunt legate prin $\ zeta=1/\xi$. Punctul în care $\xi =0$ ar trebui să aibă atunci valoarea $\zeta$ „$1/0$”. În acest sens, originea reprezentării $\xi$ joacă rolul de $\infty$ în diagrama $\zeta$. Simetric, originea reprezentării $\zeta$ joacă rolul de $\infty$ în diagrama $\xi$.

Topologic, spațiul rezultat este compactificarea^⁠(d) într-un punct a unui plan în sferă. Totuși, sfera Riemann nu este doar o sferă topologică. Este o sferă cu o structură complexă bine definită, astfel încât în jurul fiecărui punct al sferei există o vecinătate care poate fi identificată biolomorfic cu $\mathbb {C}$.

Pe de altă parte, teorema de uniformizare^⁠(d), un rezultat central în clasificarea suprafețelor Riemann, afirmă că fiecare suprafață Riemann simplu conexă este biolomorfă cu planul complex, planul hiperbolic sau sfera Riemann. Dintre acestea, sfera Riemann este singura care este o suprafață închisă (o suprafață compactă fără frontieră). Prin urmare, sfera bidimensională admite o structură complexă unică, transformând-o într-o varietate complexă unidimensională.

Ca dreaptă proiectivă complexă

Sfera Riemann poate fi definită și ca dreaptă proiectivă complexă. Punctele dreptei proiective complexe pot fi definite drept clase de echivalență^⁠(d) ale vectorilor nenuli în spațiul vectorial complex $\mathbb {C} ^{2}$: doi vectori nenuli $(w,z)$ și $(u,v)$ sunt echivalenți dacă și numai dacă $(w,z)=(\lambda u,\lambda v)$ pentru un coeficient $\lambda \in \mathbb {C}$ nenul.

În acest caz, clasa de echivalență este notată $[w,z]$ folosind coordonate proiective. Fiind dat un punct $[w,z]$ pe dreapta proiectivă complexă, unul dintre $w$ și $z$ trebuie să fie diferit de zero, fie $w\neq 0$. Apoi, prin noțiunea de echivalență, $[w,z]=\left[1,z/w\right]$, care este într-o reprezentare a varietății sferei Riemann.

Această tratare a sferei Riemann se conectează cel mai ușor cu geometria proiectivă. De exemplu, orice dreaptă (sau conică netedă^⁠(d)) din planul proiectiv complex este biolomorfă cu dreapta proiectivă complexă. De asemenea, este convenabil pentru studierea automorfismelor sferei, inclusiv în acest articol.

Ca sferă

Proiecție stereografică a unui număr complex A pe un punct α al sferei Riemann

Sfera Riemann poate fi vizualizată ca sfera unitate $x^{2}+y^{2}+z^{2}=1$ în spațiul real tridimensional $\mathbb {R} ^{3}$. În acest scop, se consideră proiecția stereografică din sfera unitate minus punctul $(0,0,1)$ pe planul $z=0$, identificat cu planul complex $\zeta =x+iy$. În coordonatele carteziene $(x,y,z)$ și coordonatele sferice $(\theta ,\phi )$ pe sferă (cu $\theta$ unghiul zenital și $\phi$ azimutul), proiecția este

$\zeta ={\frac {x+iy}{1-z}}=\cot \left({\frac {1}{2}}\theta \right)\;e^{i\phi }.$

Similar, proiecția stereografică de la $(0,0,-1)$ pe planul $z=0$, identificat cu o altă copie a planului complex prin $\xi =x-iy$, este

$\xi ={\frac {x-iy}{1+z}}=\tan \left({\frac {1}{2}}\theta \right)\;e^{-i\phi }.$

Pentru a acoperi sfera unitate sunt necesare cele două proiecții stereografice: prima va acoperi întreaga sferă, cu excepția punctului $(0,0,1)$ iar a doua cu excepția punctului $(0,0,-1)$. Prin urmare, este nevoie de două plane complexe, câte unul pentru fiecare proiecție, care pot fi văzute intuitiv ca fiind „lipite” spate în spate în $z=0$. De reținut că cele două plane complexe sunt identificate diferit cu planul $z=0$. Pentru a menține o orientare consistentă pe sferă este necesară o orientare cu inversare. În particular, conjugarea complexă face ca aplicațiile de tranziție să fie olomorfe.

Aplicațiile de tranziție între coordonatele $\zeta$ și coordonatele $\xi$ sunt obținute prin compunerea unei proiecții cu inversa celeilalte. Se dovedesc a fi $\zeta =1/\xi$ și $\xi =1/\zeta$ cum sunt descrise mai sus. Astfel, sfera unitate este difeomorfă cu sfera Riemann.

În cadrul acestui difeomorfism cercul unitate din diagrama $\zeta$, cercul unitate din diagrama $\xi$ și ecuatorul sferei unitate sunt toate identificate (unul și același). Discul unitate $|\zeta |<1$ este identic cu emisfera sudică $z<0$, în timp ce discul unitate $|\xi |<1$ este identic cu emisfera nordică $z>0$.

Metrică

O suprafață Riemann nu este echipată cu vreo metrică riemanniană. Structura conformă a suprafeței Riemann determină totuși o clasă de metrici: toate acelea a căror structură conformă subordonată este cea dată. Mai detaliat: structura complexă a suprafeței Riemann determină în mod unic o metrică până la echivalența conformă^⁠(d). (Se spune că două metrici sunt echivalente conform dacă diferă prin înmulțire cu o funcție netedă^⁠(d) pozitivă.) În schimb, orice metrică de pe o suprafață orientată^⁠(d) determină în mod unic o structură complexă, care depinde de metrică doar până la echivalența conformă. Structurile complexe de pe o suprafață orientată sunt, prin urmare, în corespondență biunivocă cu clasele conforme de metrici de pe acea suprafață.

Într-o clasă conformă dată se poate folosi simetria conformă pentru a găsi o metrică reprezentativă cu proprietăți convenabile. În special, există întotdeauna o metrică completă cu curbură constantă în orice clasă conformă dată.

În cazul sferei Riemann, teorema Gauss–Bonnet implică faptul că o metrică cu curbură constantă trebuie să aibă curbura gaussiană^⁠(d) $K$. Rezultă că prin proiecție stereografică metrica trebuie să fie izometrică față de sfera cu raza $1/{\sqrt {K}}$ în $\mathbb {R} ^{3}$. În reprezentarea $\zeta$ pe sfera Riemann, metrica cu $K=1$ este dată de

$ds^{2}=\left({\frac {2}{1+|\zeta |^{2}}}\right)^{2}\,|d\zeta |^{2}={\frac {4}{\left(1+\zeta {\overline {\zeta }}\right)^{2}}}\,d\zeta \,d{\overline {\zeta }}.$

În coordonate reale $\zeta =u+iv$, formula este

$ds^{2}={\frac {4}{\left(1+u^{2}+v^{2}\right)^{2}}}\left(du^{2}+dv^{2}\right).$

Până la un factor constant, această metrică este în acord cu metrica Fubini–Study^⁠(d) standard pentru spațiul proiectiv complex (din care sfera Riemann este un exemplu).

Până la scalare, aceasta este singura metrică de pe sferă al cărei grup de izometrii care consevă orientarea este tridimensională (și niciuna nu este mai mult decât tridimensională); acel grup se numește SO(3)^⁠(d). În acest sens, aceasta este de departe cea mai simetrică metrică de pe sferă. (Grupul tuturor izometriilor, cunoscut sub numele de O(3), este, de asemenea, tridimensional, dar, spre deosebire de ${\mbox{SO}}(3)$ nu este un spațiu conex.)

Invers, fie ca $S$ să desemneze sfera (ca o varietate netedă sau o varietate topologică^⁠(d) abstractă). Conform teoremei de uniformizare există o structură complexă unică pe $S$ până la echivalența conformă. Rezultă că orice metrică de pe $S$ este echivalentă conform cu metrica rotundă. Toate aceste metrici determină aceeași geometrie conformă. Prin urmare, metrica rotundă nu este intrinsecă sferei Riemann, deoarece „rotunjimea” nu este un invariant al geometriei conforme. Sfera Riemann este doar o varietate conformă, nu o varietate riemanniană^⁠(d). Totuși, dacă este necesară o geometrie riemanniană pe sfera Riemann, metrica rotundă este o alegere naturală (cu orice rază fixă, deși raza $1$ este cea mai simplă și mai comună alegere). Asta pentru că doar o metrică rotundă de pe sfera Riemann are grupul său de izometrie un grup tridimensional. (Și anume, grupul ${\mbox{SO}}(3)$, un grup continuu („Lie”) care topologic este spațiul proiectiv tridimensional $\mathbf {P} ^{3}$.)

Automorfisme

O transformare Möbius acționând pe sferă, respectiv pe plan prin proiecția stereografică

Articol principal: Transformare Möbius.

Studiul oricărui obiect matematic este ajutat de o înțelegere a grupului de automorfisme, adică aplicațiile de la obiect la el însuși care conservă structura esențială a obiectului. În cazul sferei Riemann, un automorfism este o aplicație conformă inversabilă (adică o aplicație biolomorfă) de la sfera Riemann la ea însăși. Se pare că singurele astfel de aplicații sunt transformările Möbius. Acestea sunt funcții de forma

$f(\zeta )={\frac {a\zeta +b}{c\zeta +d}},$

unde $a$, $b$, $c$ și $d$ sunt numere complexe astfel încât $ad-bc\neq 0$. Exemple de transformări Möbius sunt scalările, rotațiile, translațiile și inversarea complexă. De fapt, orice transformare Möbius poate fi scrisă ca o compunere a acestora.

Transformările Möbius sunt omografii^⁠(d) pe dreapta proiectivă complexă. În coordonate proiective, transformarea f poate fi scrisă

$[\zeta ,\ 1]{\begin{pmatrix}a&c\\b&d\end{pmatrix}}\ =\ [a\zeta +b,\ c\zeta +d]\ =\ \left[{\tfrac {a\zeta +b}{c\zeta +d}},\ 1\right]\ =\ [f(\zeta ),\ 1].$

Astfel, transformările Möbius pot fi descrise ca matrici complexe 2×2 cu determinantul diferit de zero. Deoarece acționează asupra coordonatelor proiective, două matrice produc aceeași transformare Möbius dacă și numai dacă diferă printr-un factor diferit de zero. Grupul transformărilor Möbius este grupul proiectiv liniar^⁠(d) ${\mbox{PGL}}(2,\mathbb {C} )$.

Dacă se înzestrează sfera Riemann cu metrica Fubini–Study, atunci nu toate transformările Möbius sunt izometrii; de exemplu, scalările și translațiile nu sunt. Izometriile formează un subgrup propriu, ${\mbox{PGL}}(2,\mathbb {C} )$, și anume ${\mbox{PSU}}(2)$. Acest subgrup este izomorf cu grupul de rotație ${\mbox{SO}}(3)$, care este grupul de simetrii al sferei unitate din $\mathbb {R} ^{3}$ (care, când se limitează la sferă, devin izometriile sferei).

Aplicații

În analiza complexă, o funcție meromorfă pe planul complex (sau pe orice suprafață Riemann) este un raport $f/g$ a două funcții olomorfe $f$ și $g$. Ca aplicație a numerelor complexe, este nedefinită oriunde $g$ este zero. Totuși, induce o aplicație olomorfă $(f,g)$ pe dreapta proiectivă complexă care este bine definită chiar și acolo unde $g=0$. Această construcție este utilă în studiul funcțiilor olomorfe și meromorfe. De exemplu, pe o suprafață compactă Riemann nu există aplicații olomorfe neconstante pentru numerele complexe, dar aplicațiile olomorfe pe dreapta proiectivă complexă sunt abundente.

Sfera Riemann are multe utilizări în fizică. În mecanica cuantică, punctele de pe dreapta proiectivă complexă sunt valori naturale pentru stările de polarizare ale fotonilor, spinul particulelor subatomice masive de spin $1/2$ și în general particule cu 2 stări (vezi și Qubit și sfera Bloch^⁠(d)). Sfera Riemann a fost sugerată ca un model relativist pentru sfera cerească. În teoria coardelor, suprafețele universului coardelor sunt suprafețe Riemann, iar sfera Riemann, fiind cea mai simplă suprafață Riemann, joacă un rol semnificativ. Este, de asemenea, importantă în teoria twistorilor^⁠(d).

Bibliografie

• en Brown, James; Churchill, Ruel (1989). Complex Variables and Applications. New York: McGraw-Hill. ISBN 0-07-010905-2. 
• en Griffiths, Phillip; Harris, Joseph (1978). Principles of Algebraic Geometry. John Wiley & Sons. ISBN 0-471-32792-1. 
• en Penrose, Roger (2005). The Road to Reality. New York: Knopf. ISBN 0-679-45443-8. 
• en Rudin, Walter (1987). Real and Complex Analysis. New York: McGraw–Hill. ISBN 0-07-100276-6. 

Legături externe

• Materiale media legate de sfera Riemann la Wikimedia Commons
• en Hazewinkel, Michiel, ed. (2001), „Riemann sphere”, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104 
• en Douglas N. Arnold, Jonathan Rogness, Moebius Transformations Revealed (a video by two University of Minnesota professors explaining and illustrating Möbius transformations using stereographic projection from a sphere)