Marea duoantiprismă
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici. |
| Marea duoantiprismă | |
 Proiecție stereografică, centrată pe o antiprismă pentagramică autointersectată | |
| Tip | 4-politop uniform |
|---|---|
| Simbol Schläfli | s{5}s{5/3} {5}⊗{5/3} h{10}s{5/3} s{5}h{10/3} h{10}h{10/3} |
| Diagramă Coxeter | |
| Celule | 50 tetraedre 10 antiprisme pentagonale 10 antiprisme pentagramice autointersectate |
| Laturi | 200 |
| Vârfuri | 50 |
| Figura vârfului | 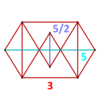 girobifastigium stelat |
| Grup Coxeter | [5,2,5]+, ordin 50 [(5,2)+,10], ordin 100 [10,2+,10], ordin 200 |
| Proprietăți | convex, tranzitiv pe vârfuri |
| Index uniform | 47 |
În geometrie marea duoantiprismă este singurul politop uniform(d) de tip duoantiprismă stelată p = 5, q = 53, din spațiul cvadridimensional. Are simbolul Schläfli {5}⊗{5/3}, s{5}s{5/3} sau ht 0,1,2,3{5,2,5/3}, diagrama Coxeter ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , fiind construită din
10 antiprisme pentagonale, 10 antiprisme pentagramice autointersectate și 50 de tetraedre. Fețele sale sunt 200 de triunghiuri, 10 pentagoane și 10 pentagrame. Vârfurile sale sunt o submulțime a vârfurilor micului 120-celule stelat.
, fiind construită din
10 antiprisme pentagonale, 10 antiprisme pentagramice autointersectate și 50 de tetraedre. Fețele sale sunt 200 de triunghiuri, 10 pentagoane și 10 pentagrame. Vârfurile sale sunt o submulțime a vârfurilor micului 120-celule stelat.

(în spațiu, celulele se suprapun)

Construcție
modificareMarea duoantiprismă poate fi construită dintr-o variantă neuniformă a duoprismei 10-10/3 (o duoprismă a unui decagon și a unei decagrame) unde lungimea laturii decagramei este de aproximativ 1,618 ori (secțiunea de aur) mai mare decât lungimea laturii decagonului printr-un proces de alternare. Prismele decagonale alternează în antiprisme pentagonale, prismele decagramice alternează în antiprisme pentagramice autointersectate cu noi tetraedre regulate create în locul vârfurilor șterse. Aceasta este singura soluție uniformă pentru duoantiprisma p-q în afară de 16-celule regulat (ca o duoantiprismă 2-2).
Bibliografie
modificare- en Regular Polytopes, H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124.
- en Norman Johnson, Uniform Polytopes, Manuscript (1991)
- en Norman Johnson, The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- en Klitzing, Richard. „4D uniform polytopes (polychora) s5/3s2s5s - gudap”.
| Politopuri regulate și uniforme convexe fundamentale în dimensiunile 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Familie | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Poligoane regulate | Triunghi | Pătrat | p-gon | Hexagon | Pentagon | |||||||
| Poliedre uniforme | Tetraedru | Octaedru • Cub | Semicub | Dodecaedru • Icosaedru | ||||||||
| 4-politopuri uniforme | 5-celule | 16-celule • Tesseract | Semitesseract | 24-celule | 120-celule • 600-celule | |||||||
| 5-politopuri uniforme | 5-simplex | 5-ortoplex • 5-cub | 5-semicub | |||||||||
| 6-politopuri uniforme | 6-simplex | 6-ortoplex • 6-cub | 6-semicub | 122 • 221 | ||||||||
| 7-politopuri uniforme | 7-simplex | 7-ortoplex • 7-cub | 7-semicub | 132 • 231 • 321 | ||||||||
| 8-politopuri uniforme | 8-simplex | 8-ortoplex • 8-cub | 8-semicub | 142 • 241 • 421 | ||||||||
| 9-politopuri uniforme | 9-simplex | 9-ortoplex • 9-cub | 9-semicub | |||||||||
| 10-politopuri uniforme | 10-simplex | 10-ortoplex • 10-cub | 10-semicub | |||||||||
| n-politopuri uniforme | n-simplex | n-ortoplex • n-cub | n-semicub | 1k2 • 2k1 • k21 | n-politop pentagonal | |||||||
| Topicuri: Familii de politopuri • Politop regulat | ||||||||||||