În matematică , identitățile trigonometrice sunt egalități care implică funcții trigonometrice și sunt adevărate pentru fiecare unică valoare a variabilei care apare. Geometric, acestea sunt identități care implică funcții de unul sau mai multe unghiuri . Acestea sunt distincte de identitățile triunghiurilor, care implică atât unghiurile cât și laturile triunghiului. Acest articol acoperă doar identitățile trigonometrice.
Toate funcțiile trigonometrice de unghi θ pot fi construite geometric în termenii cercului unitate cu centrul în O . Unele dintre aceste funcții nu mai sunt folosite în prezent. Sinusul și cosinusul unor unghiuri particulare din cercul cu raza egală cu unitatea.Aceste identități sunt utilizate acolo unde apar expresii care implică funcții trigonometrice, care trebuie să fie simplificate. O aplicație importantă este aceea a integralelor care nu conțin funcții trigonometrice, dar care implică folosirea acestor funcții prin aplicarea metodei substituției variabilelor, iar apoi simplificând integrala rezultantă prin identitățile trigonometrice.
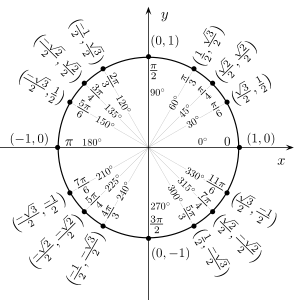
În general, pentru notația unghiurilor se folosesc literele grecești , precum alpha (α ), beta (β ), gamma (γ ), theta (θ ) etc. Sunt larg răspândite câteva modalități de măsurare a unghiurilor care folosesc unități de măsură precum radiani , grade sexagesimale și grade centezimale .
unghiul la centru corespunzător unui cerc întreg = 360° = 2
π
{\displaystyle \pi }
Următorul tablou arată conversiile pentru câteva unghiuri uzuale:
grade
30°
60°
120°
150°
210°
240°
300°
330°
Radiani
π
6
{\displaystyle {\frac {\pi }{6}}}
π
3
{\displaystyle {\frac {\pi }{3}}}
2
π
3
{\displaystyle {\frac {2\pi }{3}}}
5
π
6
{\displaystyle {\frac {5\pi }{6}}}
7
π
6
{\displaystyle {\frac {7\pi }{6}}}
4
π
3
{\displaystyle {\frac {4\pi }{3}}}
5
π
3
{\displaystyle {\frac {5\pi }{3}}}
11
π
6
{\displaystyle {\frac {11\pi }{6}}}
grade cent
33⅓ grd c
66⅔ grd c
133⅓ grd c
166⅔ grd c
233⅓ grd c
266⅔ grd c
333⅓ grd c
366⅔ grd c
grade
45°
90°
135°
180°
225°
270°
315°
360°
Radiani
π
4
{\displaystyle {\frac {\pi }{4}}}
π
2
{\displaystyle {\frac {\pi }{2}}}
3
π
4
{\displaystyle {\frac {3\pi }{4}}}
π
{\displaystyle \pi \,}
5
π
4
{\displaystyle {\frac {5\pi }{4}}}
3
π
2
{\displaystyle {\frac {3\pi }{2}}}
7
π
4
{\displaystyle {\frac {7\pi }{4}}}
2
π
{\displaystyle 2\pi \,}
grade cent
50 grd c
100 grd c
150 grd c
200 grad
250 grd c
300 grd c
350 grd c
400 grad
Dacă nu se specifică altfel, toate unghiurile din acest articol sunt date în radiani, iar unghiurile care se termină prin simbolul (°) sunt date în grade sexagesimale.
Funcțiile trigonometrice primare sunt sinusul și cosinusul unui unghi. Acestea sunt câteodată abreviate sin(θ ) și cos(θ ) , θ fiind unghiul, dar de multe ori parantezele din jurul unghiului sunt omise, scriindu-se sin θ și cos θ .
Tangenta , notată tg sau tan , unui unghi este raportul dintre sinus și cosinus:
tan
θ
=
sin
θ
cos
θ
.
{\displaystyle \tan \theta ={\frac {\sin \theta }{\cos \theta }}.}
În final putem defini funcțiile reciproce, respectiv, secanta (sec) pentru cosinus, cosecanta (cosec sau csc) pentru sinus și cotangenta (ctg sau cot) pentru tangentă:
sec
θ
=
1
cos
θ
,
csc
θ
=
1
sin
θ
,
cot
θ
=
1
tan
θ
=
cos
θ
sin
θ
.
{\displaystyle \sec \theta ={\frac {1}{\cos \theta }},\quad \csc \theta ={\frac {1}{\sin \theta }},\quad \cot \theta ={\frac {1}{\tan \theta }}={\frac {\cos \theta }{\sin \theta }}.}
Funcțiile trigonometrice inverse sunt funcții inverse parțiale ale funcțiilor trigonometrice. De exemplu, inversa funcției sinus, cunoscută ca arcsin , satisface formula:
sin
(
arcsin
x
)
=
x
{\displaystyle \sin(\arcsin x)=x\!}
iar
arcsin
(
sin
θ
)
=
θ
pentru
−
π
/
2
≤
θ
≤
π
/
2.
{\displaystyle \arcsin(\sin \theta )=\theta \quad {\text{pentru }}-\pi /2\leq \theta \leq \pi /2.}
În acest articol sunt folosite următoarele notații pentru funcțiile trigonometrice inverse:
Funcția
sin
cos
tan
sec
csc
cot
Funcția inversă
arcsin
arccos
arctan
arcsec
arccsc
arccot
Relația de bază dintre sinus și cosinus este identitatea trigonometrică a lui Pitagora:
cos
2
θ
+
sin
2
θ
=
1
{\displaystyle \cos ^{2}\theta +\sin ^{2}\theta =1\!}
Aceasta poate fi văzută ca o versiune a teoremei lui Pitagora și se deduce din ecuația x 2 + y 2 = 1 pentru cercul unitate . Această ecuație poate fi rezolvată fie pentru sinus, fie pentru cosinus:
sin
θ
=
±
1
−
cos
2
θ
și
cos
θ
=
±
1
−
sin
2
θ
.
{\displaystyle \sin \theta =\pm {\sqrt {1-\cos ^{2}\theta }}\quad {\text{și}}\quad \cos \theta =\pm {\sqrt {1-\sin ^{2}\theta }}.\,}
Divizând identitatea lui Pitagora prin cos2 θ sau sin2 θ se obțin alte două identități:
1
+
tan
2
θ
=
sec
2
θ
și
1
+
cot
2
θ
=
csc
2
θ
.
{\displaystyle 1+\tan ^{2}\theta =\sec ^{2}\theta \quad {\text{și}}\quad 1+\cot ^{2}\theta =\csc ^{2}\theta .\!}
Folosind aceste identități împreună cu identitățile de rapoarte, orice funcție trigonometrică se poate exprima în funcție de alte funcții trigonometrice (cu excepția semnului plus sau minus ):
Funcțiile versin , coversin , haversin și exsecant au fost folosite în navigație . De exemplu formula haversin-ului a fost folosită pentru a calcula distanța dintre două puncte de pe sferă. În ziua de azi au ieșit din uz și sunt foarte rar folosite.
Name(s)
Abbreviation(s)
Value [ 2]
versed sine, versin
versin
(
θ
)
{\displaystyle \operatorname {versin} (\theta )}
vers
(
θ
)
{\displaystyle \operatorname {vers} (\theta )}
ver
(
θ
)
{\displaystyle \operatorname {ver} (\theta )}
1
−
cos
(
θ
)
{\displaystyle 1-\cos(\theta )\!}
versed cosine, vercosin
vercosin
(
θ
)
{\displaystyle \operatorname {vercosin} (\theta )}
1
+
cos
(
θ
)
{\displaystyle 1+\cos(\theta )\!}
coversed sine, coversin
coversin
(
θ
)
{\displaystyle \operatorname {coversin} (\theta )}
cvs
(
θ
)
{\displaystyle \operatorname {cvs} (\theta )}
1
−
sin
(
θ
)
{\displaystyle 1-\sin(\theta )\!}
coversed cosine, covercosin
covercosin
(
θ
)
{\displaystyle \operatorname {covercosin} (\theta )}
1
+
sin
(
θ
)
{\displaystyle 1+\sin(\theta )\!}
haversed sine, haversin
haversin
(
θ
)
{\displaystyle \operatorname {haversin} (\theta )}
1
−
cos
(
θ
)
2
{\displaystyle {\frac {1-\cos(\theta )}{2}}}
haversed cosine, havercosin
havercosin
(
θ
)
{\displaystyle \operatorname {havercosin} (\theta )}
1
+
cos
(
θ
)
2
{\displaystyle {\frac {1+\cos(\theta )}{2}}}
hacoversed sine, hacoversin
hacoversin
(
θ
)
{\displaystyle \operatorname {hacoversin} (\theta )}
1
−
sin
(
θ
)
2
{\displaystyle {\frac {1-\sin(\theta )}{2}}}
hacoversed cosine, hacovercosin
hacovercosin
(
θ
)
{\displaystyle \operatorname {hacovercosin} (\theta )}
1
+
sin
(
θ
)
2
{\displaystyle {\frac {1+\sin(\theta )}{2}}}
exterior secant, exsecant
exsec
(
θ
)
{\displaystyle \operatorname {exsec} (\theta )}
sec
(
θ
)
−
1
{\displaystyle \sec(\theta )-1\!}
exterior cosecant, excosecant
excsc
(
θ
)
{\displaystyle \operatorname {excsc} (\theta )}
csc
(
θ
)
−
1
{\displaystyle \csc(\theta )-1\!}
coardă
crd
(
θ
)
{\displaystyle \operatorname {crd} (\theta )}
2
sin
(
θ
2
)
{\displaystyle 2\sin \left({\frac {\theta }{2}}\right)}
modificare
Ilustrare a formulei sumei Ilustrarea formulelor pentru sinus și cosinus, evidențiind segmentul de lungime unitate Ele au fost stabilite pentru prima dată în secolul al X-lea de matematicianul persan Abū al-Wafā' Būzjānī .
O metodă de a demonstra aceste identități este aceea de a aplica formula lui Euler .
Sinus
sin
(
α
±
β
)
=
sin
α
cos
β
±
cos
α
sin
β
{\displaystyle \sin(\alpha \pm \beta )=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \,}
[ 7] [ 8]
Cosinus
cos
(
α
±
β
)
=
cos
α
cos
β
∓
sin
α
sin
β
{\displaystyle \cos(\alpha \pm \beta )=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta \,}
[ 8] [ 9]
Tangentă
tan
(
α
±
β
)
=
tan
α
±
tan
β
1
∓
tan
α
tan
β
{\displaystyle \tan(\alpha \pm \beta )={\frac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }}}
[ 8] [ 10]
Arcsinus
arcsin
α
±
arcsin
β
=
arcsin
(
α
1
−
β
2
±
β
1
−
α
2
)
{\displaystyle \arcsin \alpha \pm \arcsin \beta =\arcsin(\alpha {\sqrt {1-\beta ^{2}}}\pm \beta {\sqrt {1-\alpha ^{2}}})}
[ 11]
Arccosinus
arccos
α
±
arccos
β
=
arccos
(
α
β
∓
(
1
−
α
2
)
(
1
−
β
2
)
)
{\displaystyle \arccos \alpha \pm \arccos \beta =\arccos(\alpha \beta \mp {\sqrt {(1-\alpha ^{2})(1-\beta ^{2})}})}
[ 12]
Arctangentă
arctan
α
±
arctan
β
=
arctan
(
α
±
β
1
∓
α
β
)
{\displaystyle \arctan \alpha \pm \arctan \beta =\arctan \left({\frac {\alpha \pm \beta }{1\mp \alpha \beta }}\right)}
[ 13]
Formulele sumei și diferenței pentru sinus și cosinus pot fi scrise sub formă matricială :
(
cos
ϕ
−
sin
ϕ
sin
ϕ
cos
ϕ
)
(
cos
θ
−
sin
θ
sin
θ
cos
θ
)
=
(
cos
ϕ
cos
θ
−
sin
ϕ
sin
θ
−
cos
ϕ
sin
θ
−
sin
ϕ
cos
θ
sin
ϕ
cos
θ
+
cos
ϕ
sin
θ
−
sin
ϕ
sin
θ
+
cos
ϕ
cos
θ
)
=
(
cos
(
θ
+
ϕ
)
−
sin
(
θ
+
ϕ
)
sin
(
θ
+
ϕ
)
cos
(
θ
+
ϕ
)
)
{\displaystyle {\begin{aligned}&{}\quad \left({\begin{array}{rr}\cos \phi &-\sin \phi \\\sin \phi &\cos \phi \end{array}}\right)\left({\begin{array}{rr}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{array}}\right)\\[12pt]&=\left({\begin{array}{rr}\cos \phi \cos \theta -\sin \phi \sin \theta &-\cos \phi \sin \theta -\sin \phi \cos \theta \\\sin \phi \cos \theta +\cos \phi \sin \theta &-\sin \phi \sin \theta +\cos \phi \cos \theta \end{array}}\right)\\[12pt]&=\left({\begin{array}{rr}\cos(\theta +\phi )&-\sin(\theta +\phi )\\\sin(\theta +\phi )&\cos(\theta +\phi )\end{array}}\right)\end{aligned}}}
modificare
sin
(
∑
i
=
1
∞
θ
i
)
=
∑
odd
k
≥
1
(
−
1
)
(
k
−
1
)
/
2
∑
A
⊆
{
1
,
2
,
3
,
…
}
|
A
|
=
k
(
∏
i
∈
A
sin
θ
i
∏
i
∉
A
cos
θ
i
)
{\displaystyle \sin \left(\sum _{i=1}^{\infty }\theta _{i}\right)=\sum _{{\text{odd}}\ k\geq 1}(-1)^{(k-1)/2}\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}\left(\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}\right)}
cos
(
∑
i
=
1
∞
θ
i
)
=
∑
even
k
≥
0
(
−
1
)
k
/
2
∑
A
⊆
{
1
,
2
,
3
,
…
}
|
A
|
=
k
(
∏
i
∈
A
sin
θ
i
∏
i
∉
A
cos
θ
i
)
{\displaystyle \cos \left(\sum _{i=1}^{\infty }\theta _{i}\right)=\sum _{{\text{even}}\ k\geq 0}~(-1)^{k/2}~~\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}\left(\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}\right)}
În aceste două identități apare o asimetrie care nu apare în cazul sumării unui număr finit de unghiuri. În fiecare produs, există numai factori sinus finiți și factori cosinus cofiniți (d
Fie e k k ∈ {0, ..., n }) polinomul simetric elementar de grad k în variabilele:
x
i
=
tan
θ
i
{\displaystyle x_{i}=\tan \theta _{i}\,}
pentru i ∈ {0, ..., n }, adică:
e
0
=
1
e
1
=
∑
1
≤
i
≤
n
x
i
=
∑
1
≤
i
≤
n
tan
θ
i
e
2
=
∑
1
≤
i
<
j
≤
n
x
i
x
j
=
∑
1
≤
i
<
j
≤
n
tan
θ
i
tan
θ
j
e
3
=
∑
1
≤
i
<
j
<
k
≤
n
x
i
x
j
x
k
=
∑
1
≤
i
<
j
<
k
≤
n
tan
θ
i
tan
θ
j
tan
θ
k
⋮
⋮
{\displaystyle {\begin{aligned}e_{0}&=1\\[6pt]e_{1}&=\sum _{1\leq i\leq n}x_{i}&&=\sum _{1\leq i\leq n}\tan \theta _{i}\\[6pt]e_{2}&=\sum _{1\leq i<j\leq n}x_{i}x_{j}&&=\sum _{1\leq i<j\leq n}\tan \theta _{i}\tan \theta _{j}\\[6pt]e_{3}&=\sum _{1\leq i<j<k\leq n}x_{i}x_{j}x_{k}&&=\sum _{1\leq i<j<k\leq n}\tan \theta _{i}\tan \theta _{j}\tan \theta _{k}\\&{}\ \ \vdots &&{}\ \ \vdots \end{aligned}}}
Atunci
tan
(
θ
1
+
⋯
+
θ
n
)
=
e
1
−
e
3
+
e
5
−
⋯
e
0
−
e
2
+
e
4
−
⋯
,
{\displaystyle \tan(\theta _{1}+\cdots +\theta _{n})={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }},}
numărul de termeni depinzând de n .
De exemplu:
tan
(
θ
1
+
θ
2
)
=
e
1
e
0
−
e
2
=
x
1
+
x
2
1
−
x
1
x
2
=
tan
θ
1
+
tan
θ
2
1
−
tan
θ
1
tan
θ
2
,
tan
(
θ
1
+
θ
2
+
θ
3
)
=
e
1
−
e
3
e
0
−
e
2
=
(
x
1
+
x
2
+
x
3
)
−
(
x
1
x
2
x
3
)
1
−
(
x
1
x
2
+
x
1
x
3
+
x
2
x
3
)
,
tan
(
θ
1
+
θ
2
+
θ
3
+
θ
4
)
=
e
1
−
e
3
e
0
−
e
2
+
e
4
=
(
x
1
+
x
2
+
x
3
+
x
4
)
−
(
x
1
x
2
x
3
+
x
1
x
2
x
4
+
x
1
x
3
x
4
+
x
2
x
3
x
4
)
1
−
(
x
1
x
2
+
x
1
x
3
+
x
1
x
4
+
x
2
x
3
+
x
2
x
4
+
x
3
x
4
)
+
(
x
1
x
2
x
3
x
4
)
,
{\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2})&={\frac {e_{1}}{e_{0}-e_{2}}}={\frac {x_{1}+x_{2}}{1\ -\ x_{1}x_{2}}}={\frac {\tan \theta _{1}+\tan \theta _{2}}{1\ -\ \tan \theta _{1}\tan \theta _{2}}},\\\\\tan(\theta _{1}+\theta _{2}+\theta _{3})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\\\\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\\\&={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}}
și așa mai departe. Cazul general poate fi demonstrat prin inducție matematică .
sec
(
θ
1
+
⋯
+
θ
n
)
=
sec
θ
1
⋯
sec
θ
n
e
0
−
e
2
+
e
4
−
⋯
{\displaystyle \sec(\theta _{1}+\cdots +\theta _{n})={\frac {\sec \theta _{1}\cdots \sec \theta _{n}}{e_{0}-e_{2}+e_{4}-\cdots }}}
în care e k k de n variabile x i θ i i = 1, ..., n , iar numărul de termeni ai numitorului depind de n .
De exemplu,
sec
(
α
+
β
+
γ
)
=
sec
α
sec
β
sec
γ
1
−
tan
α
tan
β
−
tan
α
tan
γ
−
tan
β
tan
γ
.
{\displaystyle \sec(\alpha +\beta +\gamma )={\frac {\sec \alpha \sec \beta \sec \gamma }{1-\tan \alpha \tan \beta -\tan \alpha \tan \gamma -\tan \beta \tan \gamma }}.}
Tn este polinomul Cebîșev de grad n
cos
n
θ
=
T
n
(
cos
θ
)
{\displaystyle \cos n\theta =T_{n}(\cos \theta )\,}
[ 14]
S n polinomul de dispersie de grad n
sin
2
n
θ
=
S
n
(
sin
2
θ
)
{\displaystyle \sin ^{2}n\theta =S_{n}(\sin ^{2}\theta )\,}
Formula lui Moivre ,
i
{\displaystyle i}
unitatea imaginară
cos
n
θ
+
i
sin
n
θ
=
(
cos
(
θ
)
+
i
sin
(
θ
)
)
n
{\displaystyle \cos n\theta +i\sin n\theta =(\cos(\theta )+i\sin(\theta ))^{n}\,}
[ 15]
1
+
2
cos
(
x
)
+
2
cos
(
2
x
)
+
2
cos
(
3
x
)
+
⋯
+
2
cos
(
n
x
)
=
sin
(
(
n
+
1
2
)
x
)
sin
(
x
/
2
)
.
{\displaystyle 1+2\cos(x)+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin(x/2)}}.}
Această funcție de x fiind nucleul lui Dirichlet .
Acestea pot fi obținute fie din identitățile sumei și diferenței, sau din formulelor multiplilor unghiurilor:
Formula unghiului dublu[ 16] [ 17]
sin
2
θ
=
2
sin
θ
cos
θ
=
2
tan
θ
1
+
tan
2
θ
{\displaystyle {\begin{aligned}\sin 2\theta &=2\sin \theta \cos \theta \ \\&={\frac {2\tan \theta }{1+\tan ^{2}\theta }}\end{aligned}}}
cos
2
θ
=
cos
2
θ
−
sin
2
θ
=
2
cos
2
θ
−
1
=
1
−
2
sin
2
θ
=
1
−
tan
2
θ
1
+
tan
2
θ
{\displaystyle {\begin{aligned}\cos 2\theta &=\cos ^{2}\theta -\sin ^{2}\theta \\&=2\cos ^{2}\theta -1\\&=1-2\sin ^{2}\theta \\&={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}\end{aligned}}}
tan
2
θ
=
2
tan
θ
1
−
tan
2
θ
{\displaystyle \tan 2\theta ={\frac {2\tan \theta }{1-\tan ^{2}\theta }}\,}
cot
2
θ
=
cot
2
θ
−
1
2
cot
θ
{\displaystyle \cot 2\theta ={\frac {\cot ^{2}\theta -1}{2\cot \theta }}\,}
Formula unghiului triplu[ 14] [ 18]
sin
3
θ
=
3
sin
θ
−
4
sin
3
θ
{\displaystyle \sin 3\theta =3\sin \theta -4\sin ^{3}\theta \,}
cos
3
θ
=
4
cos
3
θ
−
3
cos
θ
{\displaystyle \cos 3\theta =4\cos ^{3}\theta -3\cos \theta \,}
tan
3
θ
=
3
tan
θ
−
tan
3
θ
1
−
3
tan
2
θ
{\displaystyle \tan 3\theta ={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}}
cot
3
θ
=
3
cot
θ
−
cot
3
θ
1
−
3
cot
2
θ
{\displaystyle \cot 3\theta ={\frac {3\cot \theta -\cot ^{3}\theta }{1-3\cot ^{2}\theta }}}
Formula jumătății unghiului[ 19] [ 20]
sin
θ
2
=
±
1
−
cos
θ
2
{\displaystyle \sin {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1-\cos \theta }{2}}}}
cos
θ
2
=
±
1
+
cos
θ
2
{\displaystyle \cos {\frac {\theta }{2}}=\pm \,{\sqrt {\frac {1+\cos \theta }{2}}}}
tan
θ
2
=
csc
θ
−
cot
θ
=
±
1
−
cos
θ
1
+
cos
θ
=
sin
θ
1
+
cos
θ
=
1
−
cos
θ
sin
θ
{\displaystyle {\begin{aligned}\tan {\frac {\theta }{2}}&=\csc \theta -\cot \theta \\&=\pm \,{\sqrt {1-\cos \theta \over 1+\cos \theta }}\\&={\frac {\sin \theta }{1+\cos \theta }}\\&={\frac {1-\cos \theta }{\sin \theta }}\end{aligned}}}
cot
θ
2
=
csc
θ
+
cot
θ
=
±
1
+
cos
θ
1
−
cos
θ
=
sin
θ
1
−
cos
θ
=
1
+
cos
θ
sin
θ
{\displaystyle {\begin{aligned}\cot {\frac {\theta }{2}}&=\csc \theta +\cot \theta \\&=\pm \,{\sqrt {1+\cos \theta \over 1-\cos \theta }}\\&={\frac {\sin \theta }{1-\cos \theta }}\\&={\frac {1+\cos \theta }{\sin \theta }}\end{aligned}}}
Faptul că formula unghiului triplu pentru sinus și cosinus implică puterile aceleiași funcții permite să se facă legătura dintre trisecțiunea unghiului cu rigla și compasul cu rezolvarea ecuației cubice , arătând că acest lucru este imposibil în general.
Există o formulă de calcul a identității trigonometrice pentru unghiul triplu, dar acesta cere găsirea rădăcinilor pentru ecuația cubică
x
3
−
3
x
+
d
4
=
0
{\displaystyle x^{3}-{\frac {3x+d}{4}}=0}
x este valoarea necunoscută a funcției sinus a unghiului, iar d este valoarea cunoscută a funcției sinus pentru unghiul triplu. Oricum, discriminantul acestei ecuații este negativ, deci ecuația are trei rădăcini reale din care numai una este soluția căutată, dar niciuna din soluții nu este reductibilă la o expresie algebrică reală, astfel că, se folosesc numere complexe intermediare ale rădăcinii cubice , care se pot exprima numai prin termenii reali ai funcțiilor, folosind funcții hiperbolice .
modificare
Pentru unghiuri multiple specifice, acestea rezultă din formulele specifice de adunare a unghiurilor, în timp ce formula generală a fost găsita de matematicianul francez François Viète .
sin
n
θ
=
∑
k
=
0
n
(
n
k
)
cos
k
θ
sin
n
−
k
θ
sin
(
1
2
(
n
−
k
)
π
)
{\displaystyle \sin n\theta =\sum _{k=0}^{n}{\binom {n}{k}}\cos ^{k}\theta \,\sin ^{n-k}\theta \,\sin \left({\frac {1}{2}}(n-k)\pi \right)}
cos
n
θ
=
∑
k
=
0
n
(
n
k
)
cos
k
θ
sin
n
−
k
θ
cos
(
1
2
(
n
−
k
)
π
)
{\displaystyle \cos n\theta =\sum _{k=0}^{n}{\binom {n}{k}}\cos ^{k}\theta \,\sin ^{n-k}\theta \,\cos \left({\frac {1}{2}}(n-k)\pi \right)}
tan nθ poate fi scrisă în funcție de tan θ folosind relația de recurență:
tan
(
n
+
1
)
θ
=
tan
n
θ
+
tan
θ
1
−
tan
n
θ
tan
θ
.
{\displaystyle \tan \,(n{+}1)\theta ={\frac {\tan n\theta +\tan \theta }{1-\tan n\theta \,\tan \theta }}.}
iar cot nθ poate fi scrisă în funcție de cot θ folosind relația de recurență:
cot
(
n
+
1
)
θ
=
cot
n
θ
cot
θ
−
1
cot
n
θ
+
cot
θ
.
{\displaystyle \cot \,(n{+}1)\theta ={\frac {\cot n\theta \,\cot \theta -1}{\cot n\theta +\cot \theta }}.}
Metoda Cebîșev este un algoritm recursiv pentru a afla formula celui de al n -lea multiplu al unui unghi cunoscând formulele pentru al (n − 1)-lea și al (n − 2)-lea.[ 21]
Cosinusul pentru nx poate fi calculat din cosinusurile pentru (n − 1)x și (n − 2)x după cum urmează:
cos
n
x
=
2
⋅
cos
x
⋅
cos
(
n
−
1
)
x
−
cos
(
n
−
2
)
x
{\displaystyle \cos nx=2\cdot \cos x\cdot \cos(n-1)x-\cos(n-2)x\,}
Similar sin(nx ) poate fi calculat din sinusul pentru (n − 1)x și (n − 2)x :
sin
n
x
=
2
⋅
cos
x
⋅
sin
(
n
−
1
)
x
−
sin
(
n
−
2
)
x
{\displaystyle \sin nx=2\cdot \cos x\cdot \sin(n-1)x-\sin(n-2)x\,}
Pentru tangentă este valabilă relația:
tan
n
x
=
tan
(
n
−
1
)
x
+
tan
x
1
−
tan
(
n
−
1
)
x
tan
x
{\displaystyle \tan nx={\frac {\tan(n-1)x+\tan x}{1-\tan(n-1)x\tan x}}\,}
tan
(
α
+
β
2
)
=
sin
α
+
sin
β
cos
α
+
cos
β
=
−
cos
α
−
cos
β
sin
α
−
sin
β
{\displaystyle \tan \left({\frac {\alpha +\beta }{2}}\right)={\frac {\sin \alpha +\sin \beta }{\cos \alpha +\cos \beta }}=-\,{\frac {\cos \alpha -\cos \beta }{\sin \alpha -\sin \beta }}}
Setând α sau β la 0 găsim formula uzuală a tangentei jumătății unghiului.
cos
(
θ
2
)
⋅
cos
(
θ
4
)
⋅
cos
(
θ
8
)
⋯
=
∏
n
=
1
∞
cos
(
θ
2
n
)
=
sin
(
θ
)
θ
=
sinc
θ
.
{\displaystyle \cos \left({\theta \over 2}\right)\cdot \cos \left({\theta \over 4}\right)\cdot \cos \left({\theta \over 8}\right)\cdots =\prod _{n=1}^{\infty }\cos \left({\theta \over 2^{n}}\right)={\sin(\theta ) \over \theta }=\operatorname {sinc} \,\theta .}
modificare
Identitățile produsului prin sumă pot fi demonstrate prin aplicarea formulelor de adunare și scădere a unghiurilor.
Produsul prin sumă[ 22]
cos
θ
cos
φ
=
cos
(
θ
−
φ
)
+
cos
(
θ
+
φ
)
2
{\displaystyle \cos \theta \cos \varphi ={\cos(\theta -\varphi )+\cos(\theta +\varphi ) \over 2}}
sin
θ
sin
φ
=
cos
(
θ
−
φ
)
−
cos
(
θ
+
φ
)
2
{\displaystyle \sin \theta \sin \varphi ={\cos(\theta -\varphi )-\cos(\theta +\varphi ) \over 2}}
sin
θ
cos
φ
=
sin
(
θ
+
φ
)
+
sin
(
θ
−
φ
)
2
{\displaystyle \sin \theta \cos \varphi ={\sin(\theta +\varphi )+\sin(\theta -\varphi ) \over 2}}
cos
θ
sin
φ
=
sin
(
θ
+
φ
)
−
sin
(
θ
−
φ
)
2
{\displaystyle \cos \theta \sin \varphi ={\sin(\theta +\varphi )-\sin(\theta -\varphi ) \over 2}}
Suma prin produs[ 23]
sin
θ
±
sin
φ
=
2
sin
(
θ
±
φ
2
)
cos
(
θ
∓
φ
2
)
{\displaystyle \sin \theta \pm \sin \varphi =2\sin \left({\frac {\theta \pm \varphi }{2}}\right)\cos \left({\frac {\theta \mp \varphi }{2}}\right)}
cos
θ
+
cos
φ
=
2
cos
(
θ
+
φ
2
)
cos
(
θ
−
φ
2
)
{\displaystyle \cos \theta +\cos \varphi =2\cos \left({\frac {\theta +\varphi }{2}}\right)\cos \left({\frac {\theta -\varphi }{2}}\right)}
cos
θ
−
cos
φ
=
−
2
sin
(
θ
+
φ
2
)
sin
(
θ
−
φ
2
)
{\displaystyle \cos \theta -\cos \varphi =-2\sin \left({\theta +\varphi \over 2}\right)\sin \left({\theta -\varphi \over 2}\right)}
Dacă x , y și z sunt cele trei unghiuri ale oricărui triunghi, sau cu alte cuvinte:
dacă
x
+
y
+
z
=
π
{\displaystyle \ x+y+z=\pi \ }
atunci
tan
(
x
)
+
tan
(
y
)
+
tan
(
z
)
=
tan
(
x
)
tan
(
y
)
tan
(
z
)
.
{\displaystyle {\text{ }}\tan(x)+\tan(y)+\tan(z)=\tan(x)\tan(y)\tan(z).\,}
Dacă oricare unghi x , y sau z este un unghi de 90°, ambele părți ale egalului sunt infinite, dar nu sunt nici +∞ nici −∞. Pentru scopul actual are sens doar adăugarea punctului de la infinit de pe axa reală , abordată de tan(θ) drept tan(θ), fie prin valori pozitiv crescătoare, fie prin valori negativ descrescătoare. Aceasta este compactificarea topologică a axei reale.
dacă
x
+
y
+
z
=
π
{\displaystyle \ x+y+z=\pi \ }
atunci
sin
(
2
x
)
+
sin
(
2
y
)
+
sin
(
2
z
)
=
4
sin
(
x
)
sin
(
y
)
sin
(
z
)
.
{\displaystyle {\text{ }}\sin(2x)+\sin(2y)+\sin(2z)=4\sin(x)\sin(y)\sin(z).\,}
Charles Hermite a demonstrat următoarea identitate.[ 24] a 1 , ..., a n numere complexe , fară ca două din ele să difere printr-un multiplu întreg al lui π . Fie
A
n
,
k
=
∏
1
≤
j
≤
n
j
≠
k
cot
(
a
k
−
a
j
)
{\displaystyle A_{n,k}=\prod _{\begin{smallmatrix}1\leq j\leq n\\j\neq k\end{smallmatrix}}\cot(a_{k}-a_{j})}
(în particular, A 1,1 , fiind un produs vid este 1). Atunci
cot
(
z
−
a
1
)
⋯
cot
(
z
−
a
n
)
=
cos
n
π
2
+
∑
k
=
1
n
A
n
,
k
cot
(
z
−
a
k
)
.
{\displaystyle \cot(z-a_{1})\cdots \cot(z-a_{n})=\cos {\frac {n\pi }{2}}+\sum _{k=1}^{n}A_{n,k}\cot(z-a_{k}).}
Cel mai simplu și netrivial exemplu este cazul n = 2:
cot
(
z
−
a
1
)
cot
(
z
−
a
2
)
=
−
1
+
cot
(
a
1
−
a
2
)
cot
(
z
−
a
1
)
+
cot
(
a
2
−
a
1
)
cot
(
z
−
a
2
)
{\displaystyle \cot(z-a_{1})\cot(z-a_{2})=-1+\cot(a_{1}-a_{2})\cot(z-a_{1})+\cot(a_{2}-a_{1})\cot(z-a_{2})\,}
Dacă
w
+
x
+
y
+
z
=
π
{\displaystyle w+x+y+z=\pi \,}
Atunci
sin
(
w
+
x
)
sin
(
x
+
y
)
=
sin
(
x
+
y
)
sin
(
y
+
z
)
=
sin
(
y
+
z
)
sin
(
z
+
w
)
=
sin
(
z
+
w
)
sin
(
w
+
x
)
=
sin
(
w
)
sin
(
y
)
+
sin
(
x
)
sin
(
z
)
.
{\displaystyle {\begin{aligned}{\text{Atunci}}\;&\sin(w+x)\sin(x+y)\\&{}=\sin(x+y)\sin(y+z)\\&{}=\sin(y+z)\sin(z+w)\\&{}=\sin(z+w)\sin(w+x)=\sin(w)\sin(y)+\sin(x)\sin(z).\end{aligned}}}
A patra identitate este teorema lui Ptolemeu adaptată limbajului trigonometric.
Din anumite puncte de vedere este important de știut că orice combinație liniară a undelor sinusoidale cu aceeași perioadă sau frecvență, dar defazată , este de asemenea o undă sinusoidală cu aceeași perioadă sau frecvență, dar cu alt defazaj. În cazul unei combinații liniare de unde sinus și cosinus[ 25] π/2 ):
a
sin
x
+
b
cos
x
=
a
2
+
b
2
⋅
sin
(
x
+
φ
)
{\displaystyle a\sin x+b\cos x={\sqrt {a^{2}+b^{2}}}\cdot \sin(x+\varphi )\,}
în care:
φ
=
{
arcsin
(
b
a
2
+
b
2
)
dacă
a
≥
0
,
π
−
arcsin
(
b
a
2
+
b
2
)
dacă
a
<
0
,
{\displaystyle \varphi ={\begin{cases}\arcsin \left({\frac {b}{\sqrt {a^{2}+b^{2}}}}\right)&{\text{dacă }}a\geq 0,\\\pi -\arcsin \left({\frac {b}{\sqrt {a^{2}+b^{2}}}}\right)&{\text{dacă }}a<0,\end{cases}}}
sau echivalent
φ
=
arctan
(
b
a
)
+
{
0
dacă
a
≥
0
,
π
dacă
a
<
0.
{\displaystyle \varphi =\arctan \left({\frac {b}{a}}\right)+{\begin{cases}0&{\text{ dacă }}a\geq 0,\\\pi &{\text{ dacă }}a<0.\end{cases}}}
Mai general, pentru un defazaj arbitrar:
a
sin
x
+
b
sin
(
x
+
α
)
=
c
sin
(
x
+
β
)
{\displaystyle a\sin x+b\sin(x+\alpha )=c\sin(x+\beta )\,}
în care:
c
=
a
2
+
b
2
+
2
a
b
cos
α
,
{\displaystyle c={\sqrt {a^{2}+b^{2}+2ab\cos \alpha }},\,}
iar
β
=
arctan
(
b
sin
α
a
+
b
cos
α
)
+
{
0
dacă
a
+
b
cos
α
≥
0
,
π
dacă
a
+
b
cos
α
<
0.
{\displaystyle \beta =\arctan \left({\frac {b\sin \alpha }{a+b\cos \alpha }}\right)+{\begin{cases}0&{\text{ dacă }}a+b\cos \alpha \geq 0,\\\pi &{\text{ dacă }}a+b\cos \alpha <0.\end{cases}}}
modificare
Suma sinusurilor și a cosinusurilor cu argumente în progresie aritmetica [ 26]
sin
φ
+
sin
(
φ
+
α
)
+
sin
(
φ
+
2
α
)
+
⋯
+
sin
(
φ
+
n
α
)
=
sin
(
(
n
+
1
)
α
2
)
⋅
sin
(
φ
+
n
α
2
)
sin
α
2
.
{\displaystyle \sin {\varphi }+\sin {(\varphi +\alpha )}+\sin {(\varphi +2\alpha )}+\ \cdots \ +\sin {(\varphi +n\alpha )}={\frac {\sin {\left({\frac {(n+1)\alpha }{2}}\right)}\cdot \sin {(\varphi +{\frac {n\alpha }{2}})}}{\sin {\frac {\alpha }{2}}}}.}
cos
φ
+
cos
(
φ
+
α
)
+
cos
(
φ
+
2
α
)
+
⋯
+
cos
(
φ
+
n
α
)
=
sin
(
(
n
+
1
)
α
2
)
⋅
cos
(
φ
+
n
α
2
)
sin
α
2
.
{\displaystyle \cos {\varphi }+\cos {(\varphi +\alpha )}+\cos {(\varphi +2\alpha )}+\ \cdots \ +\cos {(\varphi +n\alpha )}={\frac {\sin {\left({\frac {(n+1)\alpha }{2}}\right)}\cdot \cos {(\varphi +{\frac {n\alpha }{2}})}}{\sin {\frac {\alpha }{2}}}}.}
Pentru orice a și b :
a
cos
(
x
)
+
b
sin
(
x
)
=
a
2
+
b
2
cos
(
x
−
atan2
(
b
,
a
)
)
{\displaystyle a\cos(x)+b\sin(x)={\sqrt {a^{2}+b^{2}}}\cos(x-\operatorname {atan2} \,(b,a))\;}
în care atan2 (y , x ) este generalizarea funcției arctan(y /x ) care acoperă întreaga circumferință a cercului .
tan
(
x
)
+
sec
(
x
)
=
tan
(
x
2
+
π
4
)
.
{\displaystyle \tan(x)+\sec(x)=\tan \left({x \over 2}+{\pi \over 4}\right).}
Această identitate este convenabilă uneori când ne gândim la gudermannian , care leagă funcțiile trigonometrice de cele hiperbolice fără a recurge la numerele complexe.
Dacă x , y și z sunt trei unghiuri ale oricărui triunghi, adică x + y + z = π , atunci
cot
(
x
)
cot
(
y
)
+
cot
(
y
)
cot
(
z
)
+
cot
(
z
)
cot
(
x
)
=
1.
{\displaystyle \cot(x)\cot(y)+\cot(y)\cot(z)+\cot(z)\cot(x)=1.\,}
Dacă ƒ (x ) este o funcție rațională liniară
f
(
x
)
=
(
cos
α
)
x
−
sin
α
(
sin
α
)
x
+
cos
α
,
{\displaystyle f(x)={\frac {(\cos \alpha )x-\sin \alpha }{(\sin \alpha )x+\cos \alpha }},}
și similar
g
(
x
)
=
(
cos
β
)
x
−
sin
β
(
sin
β
)
x
+
cos
β
,
{\displaystyle g(x)={\frac {(\cos \beta )x-\sin \beta }{(\sin \beta )x+\cos \beta }},}
atunci
f
(
g
(
x
)
)
=
g
(
f
(
x
)
)
=
(
cos
(
α
+
β
)
)
x
−
sin
(
α
+
β
)
(
sin
(
α
+
β
)
)
x
+
cos
(
α
+
β
)
.
{\displaystyle f(g(x))=g(f(x))={\frac {(\cos(\alpha +\beta ))x-\sin(\alpha +\beta )}{(\sin(\alpha +\beta ))x+\cos(\alpha +\beta )}}.}
Mai concis, dacă pentru toți α avem ƒ α ƒ de mai sus, atunci:
f
α
∘
f
β
=
f
α
+
β
.
{\displaystyle f_{\alpha }\circ f_{\beta }=f_{\alpha +\beta }.\,}
Dacă x este panta unei drepte, atunci ƒ (x ) este panta rotației ei printr-un unghi −α .
arcsin
(
x
)
+
arccos
(
x
)
=
π
/
2
{\displaystyle \arcsin(x)+\arccos(x)=\pi /2\;}
arctan
(
x
)
+
arccot
(
x
)
=
π
/
2.
{\displaystyle \arctan(x)+\operatorname {arccot}(x)=\pi /2.\;}
arctan
(
x
)
+
arctan
(
1
/
x
)
=
{
π
/
2
,
if
x
>
0
−
π
/
2
,
if
x
<
0
{\displaystyle \arctan(x)+\arctan(1/x)=\left\{{\begin{matrix}\pi /2,&{\mbox{if }}x>0\\-\pi /2,&{\mbox{if }}x<0\end{matrix}}\right.}
modificare
sin
[
arccos
(
x
)
]
=
1
−
x
2
{\displaystyle \sin[\arccos(x)]={\sqrt {1-x^{2}}}\,}
tan
[
arcsin
(
x
)
]
=
x
1
−
x
2
{\displaystyle \tan[\arcsin(x)]={\frac {x}{\sqrt {1-x^{2}}}}}
sin
[
arctan
(
x
)
]
=
x
1
+
x
2
{\displaystyle \sin[\arctan(x)]={\frac {x}{\sqrt {1+x^{2}}}}}
tan
[
arccos
(
x
)
]
=
1
−
x
2
x
{\displaystyle \tan[\arccos(x)]={\frac {\sqrt {1-x^{2}}}{x}}}
cos
[
arctan
(
x
)
]
=
1
1
+
x
2
{\displaystyle \cos[\arctan(x)]={\frac {1}{\sqrt {1+x^{2}}}}}
cot
[
arcsin
(
x
)
]
=
1
−
x
2
x
{\displaystyle \cot[\arcsin(x)]={\frac {\sqrt {1-x^{2}}}{x}}}
cos
[
arcsin
(
x
)
]
=
1
−
x
2
{\displaystyle \cos[\arcsin(x)]={\sqrt {1-x^{2}}}\,}
cot
[
arccos
(
x
)
]
=
x
1
−
x
2
{\displaystyle \cot[\arccos(x)]={\frac {x}{\sqrt {1-x^{2}}}}}
modificare
Identități curioase
cos
20
∘
⋅
cos
40
∘
⋅
cos
80
∘
=
1
8
{\displaystyle \cos 20^{\circ }\cdot \cos 40^{\circ }\cdot \cos 80^{\circ }={\frac {1}{8}}}
este un caz special al unei identități care conține o variabilă:
∏
j
=
0
k
−
1
cos
(
2
j
x
)
=
sin
(
2
k
x
)
2
k
sin
(
x
)
.
{\displaystyle \prod _{j=0}^{k-1}\cos(2^{j}x)={\frac {\sin(2^{k}x)}{2^{k}\sin(x)}}.}
O identitate similară este:
cos
π
7
cos
2
π
7
cos
3
π
7
=
1
8
,
{\displaystyle \cos {\frac {\pi }{7}}\cos {\frac {2\pi }{7}}\cos {\frac {3\pi }{7}}={\frac {1}{8}},}
precum și:
sin
20
∘
⋅
sin
40
∘
⋅
sin
80
∘
=
3
8
.
{\displaystyle \sin 20^{\circ }\cdot \sin 40^{\circ }\cdot \sin 80^{\circ }={\frac {\sqrt {3}}{8}}.}
Similar:
tan
50
∘
⋅
tan
60
∘
⋅
tan
70
∘
=
tan
80
∘
.
{\displaystyle \tan 50^{\circ }\cdot \tan 60^{\circ }\cdot \tan 70^{\circ }=\tan 80^{\circ }.}
Următoarea probabil că nu este cu adevărat o generalizare a unei identități care să conțină o variabilă (vezi explicația de mai jos):
cos
24
∘
+
cos
48
∘
+
cos
96
∘
+
cos
168
∘
=
1
2
.
{\displaystyle \cos 24^{\circ }+\cos 48^{\circ }+\cos 96^{\circ }+\cos 168^{\circ }={\frac {1}{2}}.}
Dacă se consideră următoarea identitate, cu unghiurile măsurate în radiani și având valoarea 21 la numitor, obținem:
cos
(
2
π
21
)
+
cos
(
2
⋅
2
π
21
)
+
cos
(
4
⋅
2
π
21
)
{\displaystyle \cos \left({\frac {2\pi }{21}}\right)\,+\,\cos \left(2\cdot {\frac {2\pi }{21}}\right)\,+\,\cos \left(4\cdot {\frac {2\pi }{21}}\right)}
+
cos
(
5
⋅
2
π
21
)
+
cos
(
8
⋅
2
π
21
)
+
cos
(
10
⋅
2
π
21
)
=
1
2
.
{\displaystyle \,+\,\cos \left(5\cdot {\frac {2\pi }{21}}\right)\,+\,\cos \left(8\cdot {\frac {2\pi }{21}}\right)\,+\,\cos \left(10\cdot {\frac {2\pi }{21}}\right)={\frac {1}{2}}.}
Factorii 1, 2, 4 ,5 8 și 10 sunt intregi mai mici decât 21/2 și nu au factori comuni cu numarul 21.
O cale eficientă de a calcula pe π se bazează pe următoarea identitate fără variabile, datorată lui John Machin :
π
4
=
4
arctan
1
5
−
arctan
1
239
{\displaystyle {\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}}
sau, alternativ, folosind identitatea lui Leonhard Euler :
π
4
=
5
arctan
1
7
+
2
arctan
3
79
.
{\displaystyle {\frac {\pi }{4}}=5\arctan {\frac {1}{7}}+2\arctan {\frac {3}{79}}.}
modificare
Pentru câteva unghiuri simple, sinusul și cosinusul iau forma
n
/
2
{\displaystyle \scriptstyle {\sqrt {n}}/2}
n ≤ 4, care sunt ușor de memorat.
sin
0
=
sin
0
∘
=
0
/
2
=
cos
90
∘
=
cos
(
π
2
)
sin
(
π
6
)
=
sin
30
∘
=
1
/
2
=
cos
60
∘
=
cos
(
π
3
)
sin
(
π
4
)
=
sin
45
∘
=
2
/
2
=
cos
45
∘
=
cos
(
π
4
)
sin
(
π
3
)
=
sin
60
∘
=
3
/
2
=
cos
30
∘
=
cos
(
π
6
)
sin
(
π
2
)
=
sin
90
∘
=
4
/
2
=
cos
0
∘
=
cos
0
{\displaystyle {\begin{matrix}\sin 0&=&\sin 0^{\circ }&=&{\sqrt {0}}/2&=&\cos 90^{\circ }&=&\cos \left({\frac {\pi }{2}}\right)\\\\\sin \left({\frac {\pi }{6}}\right)&=&\sin 30^{\circ }&=&{\sqrt {1}}/2&=&\cos 60^{\circ }&=&\cos \left({\frac {\pi }{3}}\right)\\\\\sin \left({\frac {\pi }{4}}\right)&=&\sin 45^{\circ }&=&{\sqrt {2}}/2&=&\cos 45^{\circ }&=&\cos \left({\frac {\pi }{4}}\right)\\\\\sin \left({\frac {\pi }{3}}\right)&=&\sin 60^{\circ }&=&{\sqrt {3}}/2&=&\cos 30^{\circ }&=&\cos \left({\frac {\pi }{6}}\right)\\\\\sin \left({\frac {\pi }{2}}\right)&=&\sin 90^{\circ }&=&{\sqrt {4}}/2&=&\cos 0^{\circ }&=&\cos 0\end{matrix}}}
Raportul de aur φ:
cos
(
π
5
)
=
cos
36
∘
=
5
+
1
4
=
φ
2
{\displaystyle \cos \left({\frac {\pi }{5}}\right)=\cos 36^{\circ }={{\sqrt {5}}+1 \over 4}={\frac {\varphi }{2}}}
sin
(
π
10
)
=
sin
18
∘
=
5
−
1
4
=
φ
−
1
2
=
1
2
φ
{\displaystyle \sin \left({\frac {\pi }{10}}\right)=\sin 18^{\circ }={{\sqrt {5}}-1 \over 4}={\varphi -1 \over 2}={1 \over 2\varphi }}
Vezi și constante trigonometrice exacte .
În calculul diferențial relațiile de mai jos cer ca unghiurile să fie măsurate în radiani . Dacă funcțiile trigonometrice sunt definite în termeni geometrici, derivatele lor pot fi găsite prin verificarea a două limite. Prima este:
lim
x
→
0
sin
x
x
=
1
,
{\displaystyle \lim _{x\rightarrow 0}{\frac {\sin x}{x}}=1,}
Verificabilă prin folosirea circului unitate. De asemenea se poate aplica regula lui L'Hopital: derivata sin x este cos x , iar derivata lui x este 1, deci găsim ușor limita știind că cos 0 = 1. A doua limită este:
lim
x
→
0
1
−
cos
x
x
=
0
,
{\displaystyle \lim _{x\rightarrow 0}{\frac {1-\cos x}{x}}=0,}
Verificabilă folosind tot regula lui L'Hopital. Dacă sinus și cosinus sunt definite prin seriile lor Taylor , atunci derivatele pot fi găsite prin diferențierea termen cu termen a seriilor de puteri.
d
d
x
sin
x
=
cos
x
{\displaystyle {d \over dx}\sin x=\cos x}
Restul funcțiilor trigonometrice pot fi diferențiate folosind identitatea de mai sus și regulile de derivare :[ 32] [ 33] [ 34]
d
d
x
sin
x
=
cos
x
,
d
d
x
arcsin
x
=
1
1
−
x
2
d
d
x
cos
x
=
−
sin
x
,
d
d
x
arccos
x
=
−
1
1
−
x
2
d
d
x
tan
x
=
sec
2
x
,
d
d
x
arctan
x
=
1
1
+
x
2
d
d
x
cot
x
=
−
csc
2
x
,
d
d
x
arccot
x
=
−
1
1
+
x
2
d
d
x
sec
x
=
tan
x
sec
x
,
d
d
x
arcsec
x
=
1
|
x
|
x
2
−
1
d
d
x
csc
x
=
−
csc
x
cot
x
,
d
d
x
arccsc
x
=
−
1
|
x
|
x
2
−
1
{\displaystyle {\begin{aligned}{d \over dx}\sin x&=\cos x,&{d \over dx}\arcsin x&={1 \over {\sqrt {1-x^{2}}}}\\\\{d \over dx}\cos x&=-\sin x,&{d \over dx}\arccos x&={-1 \over {\sqrt {1-x^{2}}}}\\\\{d \over dx}\tan x&=\sec ^{2}x,&{d \over dx}\arctan x&={1 \over 1+x^{2}}\\\\{d \over dx}\cot x&=-\csc ^{2}x,&{d \over dx}\operatorname {arccot} x&={-1 \over 1+x^{2}}\\\\{d \over dx}\sec x&=\tan x\sec x,&{d \over dx}\operatorname {arcsec} x&={1 \over |x|{\sqrt {x^{2}-1}}}\\\\{d \over dx}\csc x&=-\csc x\cot x,&{d \over dx}\operatorname {arccsc} x&={-1 \over |x|{\sqrt {x^{2}-1}}}\end{aligned}}}
Identitățile integrale pot fi găsite în "Lista integralelor funcțiilor trigonometrice ". Câteva forme generice sunt listate mai jos:
∫
d
u
a
2
−
u
2
=
sin
−
1
(
u
a
)
+
C
{\displaystyle \int {\frac {du}{\sqrt {a^{2}-u^{2}}}}=\sin ^{-1}\left({\frac {u}{a}}\right)+C}
∫
d
u
a
2
+
u
2
=
1
a
tan
−
1
(
u
a
)
+
C
{\displaystyle \int {\frac {du}{a^{2}+u^{2}}}={\frac {1}{a}}\tan ^{-1}\left({\frac {u}{a}}\right)+C}
∫
d
u
u
u
2
−
a
2
=
1
a
sec
−
1
|
u
a
|
+
C
{\displaystyle \int {\frac {du}{u{\sqrt {u^{2}-a^{2}}}}}={\frac {1}{a}}\sec ^{-1}\left|{\frac {u}{a}}\right|+C}
Faptul că diferențierea funcțiilor trigonometrice sinus și cosinus rezultă din combinații liniare ale acelorași două funcții este de importanță fundamentală în multe domenii ale matematicii, precum ecuațiile diferențiale și transformata Fourier .
Funcție
Inversa funcției[ 35]
sin
θ
=
e
i
θ
−
e
−
i
θ
2
i
{\displaystyle \sin \theta ={\frac {e^{i\theta }-e^{-i\theta }}{2i}}\,}
arcsin
x
=
−
i
ln
(
i
x
+
1
−
x
2
)
{\displaystyle \arcsin x=-i\ln \left(ix+{\sqrt {1-x^{2}}}\right)\,}
cos
θ
=
e
i
θ
+
e
−
i
θ
2
{\displaystyle \cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}\,}
arccos
x
=
−
i
ln
(
x
+
x
2
−
1
)
{\displaystyle \arccos x=-i\ln \left(x+{\sqrt {x^{2}-1}}\right)\,}
tan
θ
=
e
i
θ
−
e
−
i
θ
i
(
e
i
θ
+
e
−
i
θ
)
{\displaystyle \tan \theta ={\frac {e^{i\theta }-e^{-i\theta }}{i(e^{i\theta }+e^{-i\theta })}}\,}
arctan
x
=
i
2
ln
(
i
+
x
i
−
x
)
{\displaystyle \arctan x={\frac {i}{2}}\ln \left({\frac {i+x}{i-x}}\right)\,}
csc
θ
=
2
i
e
i
θ
−
e
−
i
θ
{\displaystyle \csc \theta ={\frac {2i}{e^{i\theta }-e^{-i\theta }}}\,}
arccsc
x
=
−
i
ln
(
i
x
+
1
−
1
x
2
)
{\displaystyle \operatorname {arccsc} x=-i\ln \left({\tfrac {i}{x}}+{\sqrt {1-{\tfrac {1}{x^{2}}}}}\right)\,}
sec
θ
=
2
e
i
θ
+
e
−
i
θ
{\displaystyle \sec \theta ={\frac {2}{e^{i\theta }+e^{-i\theta }}}\,}
arcsec
x
=
−
i
ln
(
1
x
+
1
−
i
x
2
)
{\displaystyle \operatorname {arcsec} x=-i\ln \left({\tfrac {1}{x}}+{\sqrt {1-{\tfrac {i}{x^{2}}}}}\right)\,}
cot
θ
=
i
(
e
i
θ
+
e
−
i
θ
)
e
i
θ
−
e
−
i
θ
{\displaystyle \cot \theta ={\frac {i(e^{i\theta }+e^{-i\theta })}{e^{i\theta }-e^{-i\theta }}}\,}
arccot
x
=
i
2
ln
(
x
−
i
x
+
i
)
{\displaystyle \operatorname {arccot} x={\frac {i}{2}}\ln \left({\frac {x-i}{x+i}}\right)\,}
cis
θ
=
e
i
θ
{\displaystyle \operatorname {cis} \,\theta =e^{i\theta }\,}
arccis
x
=
ln
x
i
{\displaystyle \operatorname {arccis} \,x={\frac {\ln x}{i}}\,}
Nucleul lui Dirichlet Dn (x ) este funcția care apare în ambele părți ale următoarei identități:
1
+
2
cos
(
x
)
+
2
cos
(
2
x
)
+
2
cos
(
3
x
)
+
⋯
+
2
cos
(
n
x
)
=
sin
[
(
n
+
1
2
)
x
]
sin
(
x
2
)
.
{\displaystyle 1+2\cos(x)+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)={\frac {\sin \left[\left(n+{\frac {1}{2}}\right)x\right\rbrack }{\sin \left({\frac {x}{2}}\right)}}.}
Convoluția oricărei funcții integrabile de perioadă 2π cu nucleul lui Dirichlet coincide cu funcția de gradul n din aproximarea Fourier. Același lucru este valabil pentru orice funcție generalizată .
Dacă facem schimbarea de variabilă:
t
=
tan
(
x
2
)
,
{\displaystyle t=\tan \left({\frac {x}{2}}\right),}
atunci[ 36]
sin
(
x
)
=
2
t
1
+
t
2
;
cos
(
x
)
=
1
−
t
2
1
+
t
2
;
e
i
x
=
1
+
i
t
1
−
i
t
{\displaystyle \sin(x)={\frac {2t}{1+t^{2}}}{\text{ ; }}\cos(x)={\frac {1-t^{2}}{1+t^{2}}}{\text{ ; }}e^{ix}={\frac {1+it}{1-it}}}
în care
e
i
x
=
cos
(
x
)
+
i
sin
(
x
)
{\displaystyle e^{ix}=\cos(x)+i\sin(x)}
Aceste substituții sunt folositoare la transformarea funcțiilor sinus și cosinus în funcții raționale de t , pentru a găsi primitivele integralelor.
^ Abramowitz and Stegun, p. 73, 4.3.45
^ Abramowitz and Stegun, p. 78, 4.3.147
^ Abramowitz and Stegun, p. 72, 4.3.13–15
^ „The Elementary Identities” . Arhivat din original la 30 iulie 2017 . Accesat în 27 iulie 2010 . ^ Abramowitz and Stegun, p. 72, 4.3.9
^ Abramowitz and Stegun, p. 72, 4.3.7–8
^ Abramowitz and Stegun, p. 72, 4.3.16
^ a b c Eric W. Weisstein , Trigonometric Addition Formulas MathWorld .
^ Abramowitz and Stegun, p. 72, 4.3.17
^ Abramowitz and Stegun, p. 72, 4.3.18
^ Abramowitz and Stegun, p. 80, 4.4.42
^ Abramowitz and Stegun, p. 80, 4.4.43
^ Abramowitz and Stegun, p. 80, 4.4.36
^ a b Eric W. Weisstein , Multiple-Angle Formulas MathWorld .
^ Abramowitz and Stegun, p. 74, 4.3.48
^ Abramowitz and Stegun, p. 72, 4.3.24–26
^ Eric W. Weisstein , Double-Angle Formulas MathWorld .^ Abramowitz and Stegun, p. 72, 4.3.27–28
^ Abramowitz and Stegun, p. 72, 4.3.20–22
^ Eric W. Weisstein , Half-Angle Formulas MathWorld .^ Ken Ward's Mathematics Pages, http://www.trans4mind.com/personal_development/mathematics/trigonometry/multipleAnglesRecursiveFormula.htm
^ Abramowitz and Stegun, p. 72, 4.3.31–33
^ Abramowitz and Stegun, p. 72, 4.3.34–39
^ Warren P. Johnson, "Trigonometric Identities à la Hermite", American Mathematical Monthly
^ Proof at http://pages.pacificcoast.net/~cazelais/252/lc-trig.pdf Arhivat în 3 decembrie 2011 , la Wayback Machine .
^ Michael P. Knapp, Sines and Cosines of Angles in Arithmetic Progression Arhivat în 19 iulie 2011 , la Wayback Machine .
^ Abramowitz and Stegun, p. 74, 4.3.47
^ Abramowitz and Stegun, p. 71, 4.3.2
^ Abramowitz and Stegun, p. 71, 4.3.1
^ Abramowitz and Stegun, p. 75, 4.3.89–90
^ Abramowitz and Stegun, p. 85, 4.5.68–69
^ Abramowitz and Stegun, p. 77, 4.3.105–110
^ Abramowitz and Stegun, p. 82, 4.4.52–57
^ Finney, Ross (2003 ). Calculus : Graphical, Numerical, Algebraic . Glenview, Illinois: Prentice Hall. pp. 159–161. ISBN 0-13-063131-0 . ^ Abramowitz and Stegun, p. 80, 4.4.26–31
^ Abramowitz and Stegun, p. 72, 4.3.23