Marea antiprismă
| Marea antiprismă | |
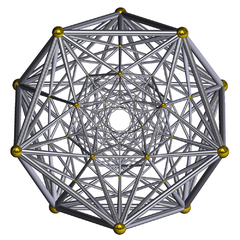 (Diagramă Schlegel, cadru de sârmă) | |
| Tip | 4-politop uniform |
|---|---|
| Celule | 100+200 de tetraedre 20 de antiprisme pentagonale |
| Fețe | 20 de pentagoane 700 de triunghiuri echilaterale |
| Laturi | 500 |
| Vârfuri | 100 |
| Figura vârfului |  sfenocoroană |
| Grup de simetrie | grup Coxeter diminuat ionic [[10,2+,10]] ordin 400 |
| Proprietăți | convex, uniform pe vârfuri |
| Index uniform | 47 |
În geometrie marea antiprismă sau antiprismoidul dublu pentagonal (nume propus de Norman Johnson) este un politop cvadridimensional, delimitat de 320 de celule: 20 de antiprisme pentagonale și 300 de tetraedre. Este un 4-politop uniform, newythoffian, anormal, descoperit în 1965 de Conway și Guy.[1][2] Din punct de vedere topologic, în cea mai mare simetrie a sa, antiprismele pentagonale au simetria D5d și există două tipuri de tetraedre, unul cu simetrie S4 și celălalt cu simetrie Cs.
Structură
modificare20 de antiprisme pentagonale apar înlănțuite în două inele disjuncte de câte 10 antiprisme fiecare. Antiprismele din fiecare inel sunt unite între ele prin fețele lor pentagonale. Cele două inele sunt reciproc perpendiculare, într-o structură asemănătoare unei duoprisme.
Cele 300 de tetraedre unesc cele două inele unul cu celălalt și sunt așezate într-un aranjament bidimensional echivalent topologic cu un 2-tor și cresta unui duocilindru. Acestea pot fi împărțite în continuare în trei seturi. Fețele a 100 dintre ele sunt în contact cu unul dintre inelele de antiprisme, fețele altor 100 sunt în contact cu celălalt inel, iar restul de 100 sunt centrate exact la mijlocul duocilindrului și laturile lor sunt în contact cu ambele inele. Acest din urmă set formează un tor plat, care poate fi „desfășurat” într-o rețea pătrată plată de tetraedre de 10×10 care se întâlnesc doar pe laturi sau vârfuri.
În plus, cele 300 de tetraedre pot fi împărțite în 10 elice Boerdijk–Coxeter de câte 30 de celule fiecare care se împletesc. Cele două inele de antiprisme pentagonale, plus cele 10 elice Boerdijk–Coxeter formează un fibrat Hopf(d) discret neregulat al marii antiprisme, care se aplică pe fețele fiecărei antiprisme pentagonale. În cele două inele de antiprisme, antiprismele sunt în contact pe fețele lor pentagonale, iar cele 10 elice Boerdijk–Coxeter vin în contact fiecare cu câte una din cele 10 fețe triunghiulare ale antiprismelor.
Structura marii antiprisme este analogă cu cea a antiprismelor tridimensionale. Totuși, marea antiprismă este singurul analog cvadridimensional uniform convex al antiprismei (deși 16-celule poate fi privit ca un analog regulat al antiprismei digonale). Singurul analog cvadridimensional uniform neconvex al antiprismei are antiprisme pentagramice autointersectate în loc de antiprisme pentagonale și se numește antiprismoid dublu pentagramic.
Figura vârfului
modificareFigura vârfului a marii antiprisme este o sfenocoroană: un icosaedru regulat cu două vârfuri adiacente eliminate. În locul lor, 8 triunghiuri sunt înlocuite cu o pereche de trapeze, cu lungimea laturilor în raporturile φ:1:1:1 (unde φ este secțiunea de aur), unite împreună de-a lungul laturii lor de lungime φ, pentru a da un tetradecaedru ale cărui fețe sunt cele 2 trapeze și cele 12 triunghiuri echilaterale rămase.
| 12 tetraedre |
2 antiprisme pentagonale |
sfenocoroană |
Construcție
modificareDupă cum se vede în imaginea desfășuratei, 600-celule regulat poate fi diminuat, adică descompus cu simetria marii antiprisme, fiecare dintre cele 20 de antiprisme pentagonale albastre fiind împărțită în 15 tetraedre regulate. Invers, cele două inele de antiprisme pentagonale din marea antiprismă pot fi triangulate de câte 10 tetraedre aflate la fețele triunghiulare ale fiecărei antiprisme și un cerc de 5 tetraedre între fiecare pereche de antiprisme, unind cele 10 tetraedre ale fiecăreia, dând 150 de tetraedre pentru fiecare inel. Acestea, combinate cu cele 300 de tetraedre care unesc cele două inele, produc cele 600 de tetraedre ale 600-celule.
Această diminuare poate fi realizată prin îndepărtarea din 600-celule a două inele de 10 vârfuri, fiecare situat în plane reciproc ortogonale. Fiecare inel de vârfuri îndepărtate creează un inel de antiprisme pentagonale pe anvelopa convexă. Această relație este analogă cu modul în care o antiprismă pentagonală poate fi construită dintr-un icosaedru prin eliminarea a două vârfuri opuse, eliminând astfel 5 triunghiuri din „polii” opuși ai icosaedrului, lăsând cele 10 triunghiuri ecuatoriale și două pentagoane în partea de sus și de jos.
Alternativ, poate fi construită și din anvelopa convexă a două duoprisme decagonale (10-10 duoprisme) perpendiculare neuniforme, unde raportul celor două decagoane este în secțiunea de aur, printr-un proces de alternare. Prismele decagonale alternează în antiprisme pentagonale, trapezoprismele dreptunghiulare alternează în tetraedre, cu două tetraedre noi, create la vârfurile omise. Aceasta este singura soluție uniformă pentru antiprismoizii dublu p-gonali alături de conjugatul său, antiprismoidul dublu pentagramic.
| 600-celule | Marea antiprismă |
|---|---|
| H4 plan Coxeter | |
| 20-gonal | |
| H3 plan Coxeter (ușor decalat) | |
Proiecții
modificareDouă proiecții în perspectivă, proiectând politopul pe o hipersferă și aplicând o proiecție stereografică în spațiul tridimensional.
| Cadru de sârmă, văzut printr-una dintre coloanele de antiprisme pentagonale. |
Cu fețele triunghiulare transparente |
| Proiecție ortogonală centrată pe hiperplanul unei antiprisme dintr-unul dintre inele |
Proiecție ortogonală 3D a 100 din cele 120 de vârfuri și 500 de laturi ale 600-celule (488 de și 12 de ) |
Note
modificare- ^ en J.H. Conway, Michael Guy, Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- ^ Conway, 2008, p.402-403 The Grand Antiprism
Bibliografie
modificare- en Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN: 978-0-471-01003-6
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591] 2.8 The Grand Antiprism
- en George Olshevsky, Anomalous convex uniform polychoron - Model 47
- en Klitzing, Richard. „4D uniform polytopes (polychora) gap”.
- en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 26) The Grand Antiprism
- en Grand Antiprism and Quaternions [1] Mehmet Koca, Mudhahir Al-Ajmi, Nazife Ozdes Koca (2009); Mehmet Koca et al. 2009 J. Phys. A: Math. Theor. 42 495201
Legături externe
modificare- en In the Belly of the Grand Antiprism[nefuncțională – arhivă] (middle section, describing the analogy with the icosahedron and the pentagonal antiprism)
| Politopuri regulate și uniforme convexe fundamentale în dimensiunile 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Familie | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Poligoane regulate | Triunghi | Pătrat | p-gon | Hexagon | Pentagon | |||||||
| Poliedre uniforme | Tetraedru | Octaedru • Cub | Semicub | Dodecaedru • Icosaedru | ||||||||
| 4-politopuri uniforme | 5-celule | 16-celule • Tesseract | Semitesseract | 24-celule | 120-celule • 600-celule | |||||||
| 5-politopuri uniforme | 5-simplex | 5-ortoplex • 5-cub | 5-semicub | |||||||||
| 6-politopuri uniforme | 6-simplex | 6-ortoplex • 6-cub | 6-semicub | 122 • 221 | ||||||||
| 7-politopuri uniforme | 7-simplex | 7-ortoplex • 7-cub | 7-semicub | 132 • 231 • 321 | ||||||||
| 8-politopuri uniforme | 8-simplex | 8-ortoplex • 8-cub | 8-semicub | 142 • 241 • 421 | ||||||||
| 9-politopuri uniforme | 9-simplex | 9-ortoplex • 9-cub | 9-semicub | |||||||||
| 10-politopuri uniforme | 10-simplex | 10-ortoplex • 10-cub | 10-semicub | |||||||||
| n-politopuri uniforme | n-simplex | n-ortoplex • n-cub | n-semicub | 1k2 • 2k1 • k21 | n-politop pentagonal | |||||||
| Topicuri: Familii de politopuri • Politop regulat | ||||||||||||